Example 10 Time-dependent reduced density
This example takes a while. I recommend execution on HPC and select JAX as wrapper
This example is the same model as Example 11.
The differences are
Example 10 employs electronic states as a direct product state.
Therefore, two MPS are simulated.
Example 11 employs electronic states as a MPS site.
Therefore, single but longer MPS is simulated.
Example 10 construct MPO by SVD while Example 11 construct MPO analytically (use symbolic scheme).
Therefore, MPO constructed in Example 11 is free from numerical error.
Example 10 is slightly accurate but Example 11 is much computationally feasible when we simulate a couple of or dozens of electronic states.
Because direct product electronic state is accurate but suffers from exponential complexity.
Furthermore, single MPS embedded in a single Array is a suitable architecture for computation.
[1]:
!nvidia-smi
zsh:1: command not found: nvidia-smi
[2]:
import platform
import sys
import pytdscf
print(sys.version)
print(f"pytdscf version = {pytdscf.__version__}")
print(platform.platform())
import jax.extend
print(jax.extend.backend.get_backend().platform)
3.12.2 (main, Feb 6 2024, 20:19:44) [Clang 15.0.0 (clang-1500.1.0.2.5)]
pytdscf version = 1.0.3
macOS-14.4.1-arm64-arm-64bit
cpu
[3]:
import matplotlib.pyplot as plt
import numpy as np
from discvar import Exponential, HarmonicOscillator, Sine
from pytdscf import BasInfo, Model, Simulator, units
from pytdscf.hamiltonian_cls import TensorHamiltonian
\[\begin{split}\begin{align}
\hat{H} &=
\left[-\frac{1}{2} \frac{\partial^2}{\partial Q_0^2}
- \frac{1}{2I} \frac{\partial^2}{\partial \theta_1^2}
- \sum_{j=2}^{24} \frac{1}{2} \frac{\partial^2}{\partial Q_{j}^2}
\right]
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\\
&+
\begin{pmatrix}
D_e\left(1-\exp\left(-\sqrt{\frac{\Omega^2}{2D_e}}Q_0^2\right)\right)^2 & \lambda Q_0 \\
\lambda Q_0 & D_e\left(1-\exp\left(-\sqrt{\frac{\Omega^2}{2D_e}}(Q_0-Q_{\mathrm{ref}})^2\right)\right)^2 +E
\end{pmatrix}
\\
&+
\begin{pmatrix}
\frac{W_0}{2}\left(1-\cos\theta_1\right) & 0\\
0 & -\frac{W_1}{2}\left(1-\cos\theta_1\right)
\end{pmatrix}
\\
&+\sum_{j=2}^{24}
\begin{pmatrix}
\frac{\omega_j^2}{2}Q_j^2 & 0 \\
0 & \frac{\omega_j^2}{2}Q_j^2+ \kappa_j Q_j
\end{pmatrix}
\end{align}\end{split}\]
References:
Morse potential is our original demonstration.
[4]:
backend = "jax"
Ω = 1532 / units.au_in_cm1 # Frequency of C=C stretching
K = 0.19 / units.au_in_eV
Q_ref = K / (Ω**1.5)
De = 2.285278e-1 # Dissociation energy 2.285278E-1 Eh = 600 kJ /mol
I = 1 / (
4.84e-04 / units.au_in_eV
) # inertial mass of C=C torsion (isomerization)
W0 = 3.56 / units.au_in_eV # isomerization term
W1 = 1.19 / units.au_in_eV # isomerization term
λ = 0.19 / units.au_in_eV # Linear vibronic coupling term
E = 2.58 / units.au_in_eV - K**2 / 2 / Ω
use_bath = True
if use_bath:
bath_ω = (
np.array(
[
792.8,
842.8,
866.2,
882.4,
970.3,
976.0,
997.0,
1017.1,
1089.6,
1189.0,
1214.7,
1238.1,
1267.9,
1317.0,
1359.0,
1389.0,
1428.4,
1434.9,
1451.8,
1572.8,
1612.1,
1629.2,
1659.1,
]
)
/ units.au_in_cm1
)
dimless_displace = np.array(
[
0.175,
0.2,
0.175,
0.225,
0.55,
0.3,
0.33,
0.45,
0.125,
0.175,
0.44,
0.5,
0.475,
0.238,
0.25,
0.25,
0.25,
0.225,
0.225,
0.25,
0.225,
0.125,
0.225,
]
) # c=κ/ω
[5]:
basis = [
Sine(ngrid=2**6, length=175.0, x0=-55.0, units="a.u."),
Exponential(ngrid=2**8 - 1, length=2 * np.pi, x0=-np.pi),
]
if use_bath:
for ω, c in zip(bath_ω, dimless_displace, strict=False):
ho_grids = HarmonicOscillator(10, ω, units="a.u.").get_grids()
left_grid = ho_grids[0] - c / np.sqrt(ω)
length = ho_grids[-1] - ho_grids[0] + c / np.sqrt(ω) ## c=κ/ω
basis.append(
Sine(ngrid=2**5, length=length, x0=left_grid, units="a.u.")
)
basinfo = BasInfo([basis, basis])
[6]:
s1_func = {}
s1_func[(0,)] = (
lambda Q0: De
* (1.0 - np.exp(-1.0 * np.sqrt(Ω**2 / 2.0 / De) * (Q0 - Q_ref))) ** 2
)
s1_func[(1,)] = lambda θ1: -W1 / 2.0 * (1.0 - np.cos(θ1))
s0_func = {}
s0_func[(0,)] = (
lambda Q0: De * (1.0 - np.exp(-1.0 * np.sqrt(Ω**2 / 2.0 / De) * Q0)) ** 2
)
s0_func[(1,)] = lambda θ1: W0 / 2.0 * (1.0 - np.cos(θ1))
v01_func = {}
v01_func[(0,)] = lambda Q0: λ * np.sqrt(Ω) * Q0
if use_bath:
for i in range(len(bath_ω)):
# Be careful to late binding
s0_func[(i + 2,)] = lambda Qi, i=i: bath_ω[i] ** 2 / 2 * Qi**2
s1_func[(i + 2,)] = (
lambda Qi, i=i: bath_ω[i] ** 2 / 2 * Qi**2
+ dimless_displace[i] * (bath_ω[i] ** 1.5) * Qi
)
[7]:
if use_bath:
plt.plot(
x := np.array(basis[2].get_grids()), (s1_func[(2,)](x)) * units.au_in_eV
)
plt.plot(
x := np.array(basis[2].get_grids()), s0_func[(2,)](x) * units.au_in_eV
)
plt.show()
[8]:
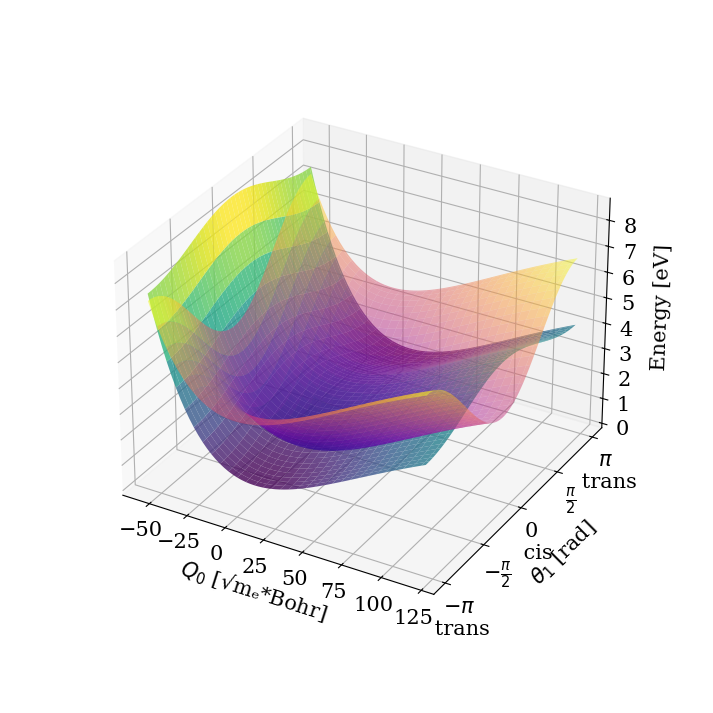
def S1(Q, θ):
return s1_func[(0,)](Q) + s1_func[(1,)](θ) + E
def S0(Q, θ):
return s0_func[(0,)](Q) + s0_func[(1,)](θ)
plt.rcParams["font.size"] = 15
plt.rcParams["font.family"] = "DejaVu Serif"
Q, θ = np.meshgrid(basis[0].get_grids(), basis[1].get_grids())
V11 = (S1(Q, θ)) * units.au_in_eV
V00 = (S0(Q, θ)) * units.au_in_eV
fig = plt.figure(figsize=(9, 9))
ax = fig.add_subplot(111, projection="3d")
ax.set_xlabel("$Q_0$ [√mₑ*Bohr]")
ax.xaxis.labelpad = 10
ax.set_ylabel(r"$\theta_1$ [rad]")
ax.yaxis.labelpad = 15
ax.set_zlabel("Energy [eV]")
ax.zaxis.labelpad = 10
ax.set_yticks(
[-np.pi, -np.pi / 2.0, 0.0, np.pi / 2.0, np.pi],
[
"$-\\pi$ \n trans",
r"$-\frac{\pi}{2}$",
"0 \n cis",
r"$\frac{\pi}{2}$",
"$\\pi$ \n trans",
],
)
surf = ax.plot_surface(Q, θ, V00, cmap="plasma", alpha=0.5)
surf = ax.plot_surface(Q, θ, V11, cmap="viridis", alpha=0.8)
ax.set_box_aspect(aspect=None, zoom=0.8)
plt.show()
[9]:
from pytdscf.dvr_operator_cls import (
TensorOperator,
construct_kinetic_operator,
construct_nMR_recursive,
)
mpo_11 = construct_nMR_recursive(basis, nMR=1, func=s1_func, rate=0.99999999999)
mpo_00 = construct_nMR_recursive(basis, nMR=1, func=s0_func, rate=0.99999999999)
mpo_01 = construct_nMR_recursive(
basis[0:1], nMR=1, func=v01_func, rate=0.99999999999
)
[10]:
# MPO has legs on (0,1,2, ... ,f-1) sites. This legs are given by tuple key
V11 = {tuple([k for k in range(len(basis))]): TensorOperator(mpo=mpo_11)}
V00 = {tuple([k for k in range(len(basis))]): TensorOperator(mpo=mpo_00)}
V01 = {(0,): TensorOperator(mpo=mpo_01, legs=(0,))}
# constant shift term is given by empty () which means no legs of tensor
# Eshift = 0.0 / units.au_in_eV
coupleJ = [[-E / 2, 0], [0, E / 2]]
V11[()] = coupleJ[1][1]
V00[()] = coupleJ[0][0]
V01[()] = coupleJ[0][1]
potential = [[V00, V01], [V01, V11]]
# Kinetic energy operator is given by
K00 = construct_kinetic_operator(
basis, coefs=[1.0, 1.0 / I] + [1.0] * (len(basis) - 2)
)
kinetic = [[K00, None], [None, K00]]
H = TensorHamiltonian(
ndof=len(basis), potential=potential, kinetic=kinetic, backend=backend
)
operators = {"hamiltonian": H}
[11]:
model = Model(basinfo=basinfo, operators=operators)
model.m_aux_max = 20
[12]:
def get_initial_state(ω, x):
weight = np.exp(-ω / 2 * (np.array(x)) ** 2)
weight /= np.linalg.norm(weight)
return weight.tolist()
ω_list = [Ω, 2 / (0.15228**2)]
if use_bath:
ω_list += bath_ω.tolist()
# I wonder where 0.15228 comes from???
# but https://pubs.acs.org/doi/epdf/10.1021/acs.jctc.2c00209 adopts this value
# as an initial Gaussian width of the torsional mode
init_vib = [
get_initial_state(ω, bas.get_grids())
for ω, bas in zip(ω_list, basis, strict=True)
]
model.init_weight_VIBSTATE = [init_vib, init_vib]
model.init_weight_ESTATE = [0.0, 1.0]
[13]:
jobname = "isomerization"
if use_bath:
jobname += "_bath"
simulator = Simulator(jobname=jobname, model=model, backend=backend, verbose=2)
simulator.propagate(
maxstep=4000,
stepsize=0.05,
reduced_density=([(0, 1)], 40),
energy=False,
autocorr=False,
)
# calculate (0,1) reduced density every 20 steps
2024-11-28 19:14:35,910 - INFO:main.pytdscf._const_cls -
____ __________ .____ ____ _____
/ _ | /__ __/ _ \ / ___ / _ \ / ___/
/ /_) /_ __/ / / / ||/ /__ / / )_// /__
/ ___/ / / / / / / / |.__ / | __/ ___/
/ / / /_/ / / / /_/ /___/ /| \_/ / /
/__/ \__, /_/ /_____/_____/ \____/_/
/____/
2024-11-28 19:14:35,910 - INFO:main.pytdscf._const_cls - Log file is ./isomerization_bath_prop/main.log
2024-11-28 19:14:35,910 - INFO:main.pytdscf.simulator_cls - Set integral of DVR basis
2024-11-28 19:14:35,911 - INFO:main.pytdscf.simulator_cls - Set initial wave function (DVR basis)
2024-11-28 19:14:35,912 - INFO:main.pytdscf.simulator_cls - Prepare MPS w.f.
2024-11-28 19:14:35,912 - INFO:main.pytdscf._mps_cls - Initial MPS: 0-state with weights 0.0
2024-11-28 19:14:35,912 - INFO:main.pytdscf._mps_cls - Initial MPS: 1-state with weights 1.0
2024-11-28 19:14:36,110 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_isomerization_bath.pkl
2024-11-28 19:14:36,127 - INFO:main.pytdscf.simulator_cls - Start initial step 0.000 [fs]
2024-11-28 19:14:56,390 - INFO:main.pytdscf.simulator_cls - End 0 step; propagated 0.050 [fs]; AVG Krylov iteration: 6.82
2024-11-28 19:19:19,408 - INFO:main.pytdscf.simulator_cls - End 100 step; propagated 5.050 [fs]; AVG Krylov iteration: 6.98
2024-11-28 19:23:23,393 - INFO:main.pytdscf.simulator_cls - End 200 step; propagated 10.050 [fs]; AVG Krylov iteration: 6.63
2024-11-28 19:27:24,833 - INFO:main.pytdscf.simulator_cls - End 300 step; propagated 15.050 [fs]; AVG Krylov iteration: 6.48
2024-11-28 19:31:25,621 - INFO:main.pytdscf.simulator_cls - End 400 step; propagated 20.050 [fs]; AVG Krylov iteration: 6.41
2024-11-28 19:35:31,346 - INFO:main.pytdscf.simulator_cls - End 500 step; propagated 25.050 [fs]; AVG Krylov iteration: 6.37
2024-11-28 19:39:31,784 - INFO:main.pytdscf.simulator_cls - End 600 step; propagated 30.050 [fs]; AVG Krylov iteration: 6.34
2024-11-28 19:43:34,072 - INFO:main.pytdscf.simulator_cls - End 700 step; propagated 35.050 [fs]; AVG Krylov iteration: 6.32
2024-11-28 19:47:34,565 - INFO:main.pytdscf.simulator_cls - End 800 step; propagated 40.050 [fs]; AVG Krylov iteration: 6.30
2024-11-28 19:51:35,803 - INFO:main.pytdscf.simulator_cls - End 900 step; propagated 45.050 [fs]; AVG Krylov iteration: 6.29
2024-11-28 19:55:36,012 - INFO:main.pytdscf.simulator_cls - Saved wavefunction 49.950 [fs]
2024-11-28 19:55:41,105 - INFO:main.pytdscf.simulator_cls - End 1000 step; propagated 50.050 [fs]; AVG Krylov iteration: 6.28
2024-11-28 19:59:53,265 - INFO:main.pytdscf.simulator_cls - End 1100 step; propagated 55.050 [fs]; AVG Krylov iteration: 6.27
2024-11-28 20:04:08,619 - INFO:main.pytdscf.simulator_cls - End 1200 step; propagated 60.050 [fs]; AVG Krylov iteration: 6.26
2024-11-28 20:08:27,947 - INFO:main.pytdscf.simulator_cls - End 1300 step; propagated 65.050 [fs]; AVG Krylov iteration: 6.25
2024-11-28 20:12:56,916 - INFO:main.pytdscf.simulator_cls - End 1400 step; propagated 70.050 [fs]; AVG Krylov iteration: 6.25
2024-11-28 20:17:25,982 - INFO:main.pytdscf.simulator_cls - End 1500 step; propagated 75.050 [fs]; AVG Krylov iteration: 6.24
2024-11-28 20:21:54,178 - INFO:main.pytdscf.simulator_cls - End 1600 step; propagated 80.050 [fs]; AVG Krylov iteration: 6.24
2024-11-28 20:26:26,032 - INFO:main.pytdscf.simulator_cls - End 1700 step; propagated 85.050 [fs]; AVG Krylov iteration: 6.23
2024-11-28 20:30:57,945 - INFO:main.pytdscf.simulator_cls - End 1800 step; propagated 90.050 [fs]; AVG Krylov iteration: 6.23
2024-11-28 20:35:37,821 - INFO:main.pytdscf.simulator_cls - End 1900 step; propagated 95.050 [fs]; AVG Krylov iteration: 6.22
2024-11-28 20:40:02,979 - INFO:main.pytdscf.simulator_cls - Saved wavefunction 99.950 [fs]
2024-11-28 20:40:08,632 - INFO:main.pytdscf.simulator_cls - End 2000 step; propagated 100.050 [fs]; AVG Krylov iteration: 6.22
2024-11-28 20:44:42,813 - INFO:main.pytdscf.simulator_cls - End 2100 step; propagated 105.050 [fs]; AVG Krylov iteration: 6.21
2024-11-28 20:49:16,184 - INFO:main.pytdscf.simulator_cls - End 2200 step; propagated 110.050 [fs]; AVG Krylov iteration: 6.21
2024-11-28 20:53:50,492 - INFO:main.pytdscf.simulator_cls - End 2300 step; propagated 115.050 [fs]; AVG Krylov iteration: 6.21
2024-11-28 20:58:25,986 - INFO:main.pytdscf.simulator_cls - End 2400 step; propagated 120.050 [fs]; AVG Krylov iteration: 6.20
2024-11-28 21:02:59,426 - INFO:main.pytdscf.simulator_cls - End 2500 step; propagated 125.050 [fs]; AVG Krylov iteration: 6.20
2024-11-28 21:07:32,594 - INFO:main.pytdscf.simulator_cls - End 2600 step; propagated 130.050 [fs]; AVG Krylov iteration: 6.19
2024-11-28 21:12:03,496 - INFO:main.pytdscf.simulator_cls - End 2700 step; propagated 135.050 [fs]; AVG Krylov iteration: 6.19
2024-11-28 21:16:32,174 - INFO:main.pytdscf.simulator_cls - End 2800 step; propagated 140.050 [fs]; AVG Krylov iteration: 6.18
2024-11-28 21:20:58,257 - INFO:main.pytdscf.simulator_cls - End 2900 step; propagated 145.050 [fs]; AVG Krylov iteration: 6.18
2024-11-28 21:25:14,970 - INFO:main.pytdscf.simulator_cls - Saved wavefunction 149.950 [fs]
2024-11-28 21:25:20,321 - INFO:main.pytdscf.simulator_cls - End 3000 step; propagated 150.050 [fs]; AVG Krylov iteration: 6.17
2024-11-28 21:29:55,630 - INFO:main.pytdscf.simulator_cls - End 3100 step; propagated 155.050 [fs]; AVG Krylov iteration: 6.16
2024-11-28 21:34:42,623 - INFO:main.pytdscf.simulator_cls - End 3200 step; propagated 160.050 [fs]; AVG Krylov iteration: 6.15
2024-11-28 21:39:13,709 - INFO:main.pytdscf.simulator_cls - End 3300 step; propagated 165.050 [fs]; AVG Krylov iteration: 6.14
2024-11-28 21:44:03,088 - INFO:main.pytdscf.simulator_cls - End 3400 step; propagated 170.050 [fs]; AVG Krylov iteration: 6.12
2024-11-28 21:48:35,322 - INFO:main.pytdscf.simulator_cls - End 3500 step; propagated 175.050 [fs]; AVG Krylov iteration: 6.11
2024-11-28 21:52:46,160 - INFO:main.pytdscf.simulator_cls - End 3600 step; propagated 180.050 [fs]; AVG Krylov iteration: 6.10
2024-11-28 21:56:57,399 - INFO:main.pytdscf.simulator_cls - End 3700 step; propagated 185.050 [fs]; AVG Krylov iteration: 6.09
2024-11-28 22:01:09,593 - INFO:main.pytdscf.simulator_cls - End 3800 step; propagated 190.050 [fs]; AVG Krylov iteration: 6.07
2024-11-28 22:05:19,055 - INFO:main.pytdscf.simulator_cls - End 3900 step; propagated 195.050 [fs]; AVG Krylov iteration: 6.06
2024-11-28 22:09:28,889 - INFO:main.pytdscf.simulator_cls - Saved wavefunction 199.950 [fs]
2024-11-28 22:09:31,465 - INFO:main.pytdscf.simulator_cls - End 3999 step; propagated 199.950 [fs]; AVG Krylov iteration: 6.05
2024-11-28 22:09:31,466 - INFO:main.pytdscf.simulator_cls - End simulation and save wavefunction
2024-11-28 22:09:31,517 - INFO:main.pytdscf.simulator_cls - Wave function is saved in wf_isomerization_bath.pkl
[13]:
(None, <pytdscf.wavefunction.WFunc at 0x149a6fc80>)
[14]:
import netCDF4 as nc
from matplotlib.animation import FuncAnimation
with nc.Dataset(f"{jobname}_prop/reduced_density.nc", "r") as file:
density_data_S1 = file.variables["rho_(0, 1)_1"][:]["real"]
density_data_S0 = file.variables["rho_(0, 1)_0"][:]["real"]
time_data = file.variables["time"][:]
print(time_data.shape)
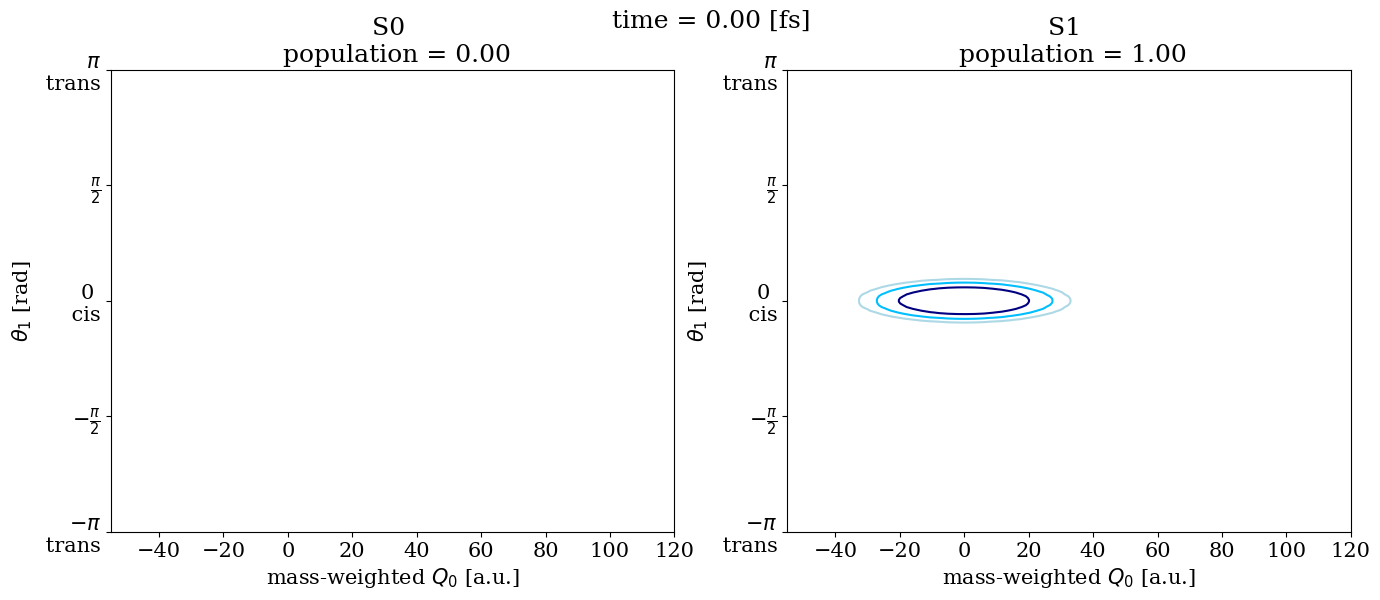
fig, (ax0, ax1) = plt.subplots(1, 2, figsize=(16, 6))
def update(i):
ax0.cla()
ax1.cla()
im0 = ax0.contour(
Q,
θ,
density_data_S0[i, :, :].T,
levels=[1.0e-05, 1.0e-04, 1.0e-03],
colors=["lightblue", "deepskyblue", "navy"],
)
# cmap='jet', vmin=0, vmax=0.05, )
im1 = ax1.contour(
Q,
θ,
density_data_S1[i, :, :].T,
levels=[1.0e-05, 1.0e-04, 1.0e-03],
colors=["lightblue", "deepskyblue", "navy"],
)
# fix coordinate of title
fig.suptitle(f"time = {time_data[i]:4.2f} [fs]")
ax0.set_title(f"S0 \n population = {np.sum(density_data_S0[i]):0.2f}")
ax1.set_title(f"S1 \n population = {np.sum(density_data_S1[i]):0.2f}")
ax0.set_xlabel("mass-weighted $Q_0$ [a.u.]")
ax1.set_xlabel("mass-weighted $Q_0$ [a.u.]")
ax0.set_ylabel(r"$\theta_1$ [rad]")
ax1.set_ylabel(r"$\theta_1$ [rad]")
ax0.set_yticks(
[-np.pi, -np.pi / 2.0, 0.0, np.pi / 2.0, np.pi],
[
"$-\\pi$ \n trans",
r"$-\frac{\pi}{2}$",
"0 \n cis",
r"$\frac{\pi}{2}$",
"$\\pi$ \n trans",
],
)
ax1.set_yticks(
[-np.pi, -np.pi / 2.0, 0.0, np.pi / 2.0, np.pi],
[
"$-\\pi$ \n trans",
r"$-\frac{\pi}{2}$",
"0 \n cis",
r"$\frac{\pi}{2}$",
"$\\pi$ \n trans",
],
)
return im0, im1
anim = FuncAnimation(fig, update, frames=range(0, len(time_data)), interval=100)
if use_bath:
gif_name = "reduced_density_bath.gif"
else:
gif_name = "reduced_density_zerotemp.gif"
anim.save(gif_name, writer="pillow")
(100,)
