Example 12 Singlet fission with bath modes

This example takes a while. (a couple of hours)

• References

  • Chin, Alex W., et al. “Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials.” Journal of Mathematical Physics 51.9 (2010).

  • Zheng, Jie, et al. “Ultrafast nonadiabatic dynamics of singlet fission: Quantum dynamics with the multilayer multiconfigurational time-dependent Hartree (ML-MCTDH) method.” The Journal of Physical Chemistry C 120.3 (2016): 1375-1389.

import platform
import sys

import pytdscf

print(sys.version)
print(f"pytdscf version = {pytdscf.__version__}")
print(platform.platform())

import jax.extend

print(jax.extend.backend.get_backend().platform)

3.13.2 (main, Feb  4 2025, 14:51:09) [Clang 16.0.0 (clang-1600.0.26.6)]
pytdscf version = 1.1.0
macOS-15.4.1-arm64-arm-64bit-Mach-O
cpu

import math

import matplotlib.pyplot as plt
import numpy as np
import sympy
from pympo import AssignManager, OpSite, SumOfProducts
from pympo.utils import export_npz

from pytdscf import (
    BasInfo,
    Boson,
    Exciton,
    Model,
    Simulator,
    TensorHamiltonian,
    TensorOperator,
    units,
)

Model Hamiltonian

\[H = H_{\text{ele}} + H_{\text{ph}} + H_{\text{el-ph}}\]

where \(H_{\text{ele}}\) is the electronic Hamiltonian consisting of three sites (S1, TT, CT in this order) and represented by following effective Hamiltonian

\[\begin{split}H_{\text{ele}} = \begin{pmatrix} 0.2 & 0 & -0.05 \\ 0 & 0 & -0.05 \\ -0.05 & -0.05 & 0.3 \end{pmatrix}\end{split}\]

and \(H_{\text{ph}}\) and \(H_{\text{el-ph}}\) are the phonon and electron-phonon coupling Hamiltonians, respectively.

\[H_{\text{ph}} + H_{\text{el-ph}} = \sum_{k} |k\rangle \langle k| c_0 (b_0 + b_0^\dagger) + \sum_{n=1}^N (\omega_n b_n^\dagger b_n + t_n b_{n+1}^\dagger b_n + t_n b_n^\dagger b_{n+1})\]

For detail derivation of this reserovir model, please refer to the reference.

We will set the electronic state as the left terminal site (i=0) and the bath modes as i=1 to N+1 sites.

Spectral density

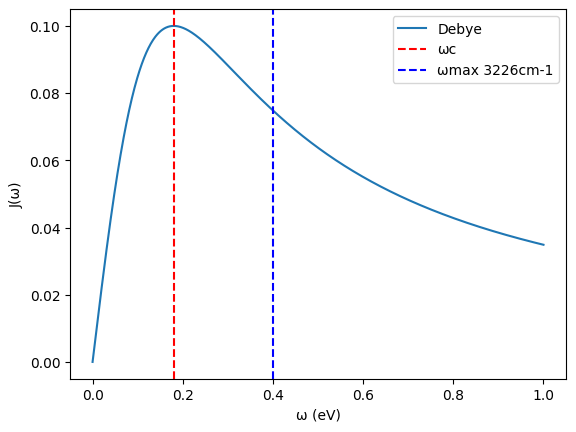
The previous study employed the spectral density defined as Debye type (Lorentzian decaying)

\[J_{\text{Debye}}(\omega) = \frac{2\lambda \omega \omega_c}{\omega_c^2 + \omega^2}\]

with a finite cutoff frequency \(\omega_{\text{max}}\).

ωc = 0.18  # eV a.k.a charactaristic frequency
λ = 0.10  # eV a.k.a reorganization energy
ωmax = 0.40


def J_debye(ω):
    return 2 * λ * ω * ωc / (ω * ω + ωc * ωc)


omega = np.linspace(0.0, 1.0, 1000)
plt.plot(omega, J_debye(omega), label="Debye")
plt.xlabel("ω (eV)")
plt.ylabel("J(ω)")
plt.axvline(x=ωc, color="red", linestyle="--", label="ωc")
plt.axvline(x=ωmax, color="blue", linestyle="--", label="ωmax 3226cm-1")
plt.legend()
plt.show()

The easiest transformation to finite number of harmonic oscillators is just discretizing integral

\[\begin{split}\begin{align} & H_{\text{sys}} + H_{\text{res}} + V \\ &= H_{\text{sys}} + \int_0^{x_{\text{max}}} dx g(x) a_{x} a_{x}^\dagger + \int_0^{x_{\text{max}}} dx h(x) \hat{A} (a_{x} + a_{x}^\dagger) \\ &\approx H_{\text{sys}} + \sum_{n=1}^N \omega_n a_n^\dagger a_n + \sum_{n=1}^N c_n \hat{A} (a_n + a_n^\dagger) \end{align}\end{split}\]

\(N\) is usually required to be a hundred number to represent the continuous spectral density.

However, there exists a more sophisticated method to map the continuous spectral density to the discrete chain with nearest neighbor coupling.

Orthogonal polynomial mapping

We will define spectral density as

\[J(\omega) = \frac{2\lambda \frac{\omega}{\omega_c}}{1+\left(\frac{\omega}{\omega_c}\right)^2} \theta\left(\frac{\omega}{\omega_{\text{max}}} - 1\right)\]

where \(\theta(x)\) is the Heaviside step function. When we set \(g(x) = \omega_{\text{max}} x\) and \(x_{\text{max}}=1\), from the following relation

\[J(\omega) = \pi h^2\left(\frac{\omega}{\omega_{\text{max}}}\right) \frac{1}{\omega_{\text{max}}},\]

we can extract constant \(C=2\lambda\omega_c / \pi\) and define measure

\[\mu(x) := \frac{h^2(x)}{C} = \frac{x}{\frac{1}{L^2}+x^2} \quad \left(0<x<1, L=\frac{\omega_{\text{max}}}{\omega_c}\right)\]

and orthogonal monic polynomials \(\{\pi_n\}\) which satisfy

\[\Braket{\pi_n,\pi_m}_{\mu} = \int_0^1 \pi_n(x) \pi_m(x) \mu(x) dx = \delta_{nm} ||\pi_n||^2\]

and

\[\pi_{n+1} = (x-\alpha_n) \pi_n - \beta_n \pi_{n-1}\]

where \(\pi_0 = 1\) and \(\pi_{-1} = 0\).

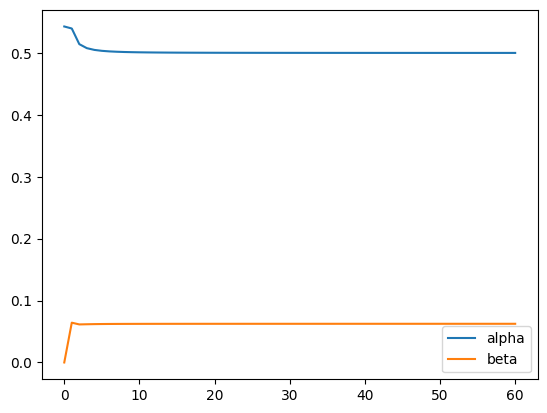
The goal is to find recursion coefficients \(\alpha_n\) and \(\beta_n\) which satisfy

\[\alpha_n = \frac{\Braket{x\pi_n, \pi_n}_{\mu}}{\Braket{\pi_n, \pi_n}_{\mu}}\]

and

\[\beta_n = \frac{\Braket{\pi_n, \pi_n}_{\mu}}{\Braket{\pi_{n-1}, \pi_{n-1}}_{\mu}}.\]

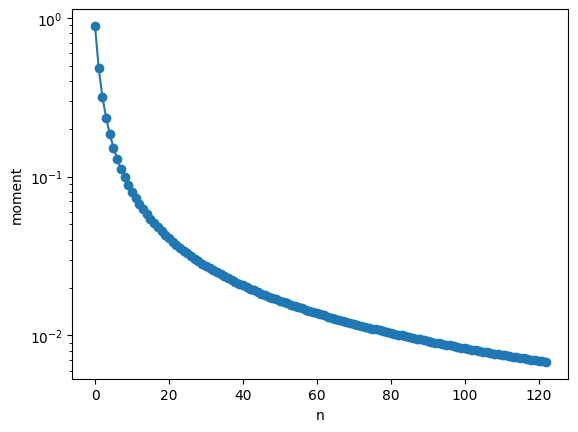
First we need to prepare the \(k\)-th moment of the measure up to \(k=2N\).

\[m_k = \int_0^1 x^k \mu(x) dx = \int_0^1 \frac{x^{k+1}}{\frac{1}{L^2}+x^2} dx = L\int_0^{\arctan L} \left(\frac{\tan\theta}{L}\right)^{k+1} d\theta\]

\[m_k = \frac{1}{k} - \frac{1}{L^2}m_{k-2}, \quad m_0 = -\log(\cos(\arctan(L))) = \frac{1}{2} \log(1+L^2) , \quad m_1 = 1 - \frac{1}{L}\arctan L\]

Then, we determine the coefficients \(\alpha_n\) and \(\beta_n\) recursively.

Note that recursive calculation tends to accumulate errors, so we will use mpmath to calculate the coefficients. (If you don’t have, install mpmath)

from mpmath import mp, mpf

mp.dps = 512


def get_momments(n_order, L: float):
    moments = [
        mpf(1) / mpf(2) * mp.log1p(mpf(L) ** 2),
        1 - mp.atan(mpf(L)) / mpf(L),
    ]
    for k in range(2, 2 * n_order + 1):
        moments.append(1 / mpf(k) - moments[-2] / mpf(L) / mpf(L))
    return moments


n_order = 61
L = ωmax / ωc
moments = get_momments(n_order, L)

plt.plot(moments, marker="o")
plt.xlabel("n")
plt.ylabel("moment")
plt.yscale("log")
plt.axhline(0.0, color="black", linestyle="--")
plt.show()

def polynomial_inner_product(
    poly1: np.ndarray, poly2: np.ndarray, moments: np.ndarray
):
    """
    Calculate the inner product of two polynomials using the moments.

    Args:
        poly1: Coefficients of the first polynomial. [1.0, 2.0, 3.0] means 1 + 2x + 3x^2
        poly2: Coefficients of the second polynomial. [1.0, 2.0, 3.0] means 1 + 2x + 3x^2
        moments: Moments used to calculate the inner product.
    """
    assert len(poly1) + len(poly2) - 1 <= len(moments)
    # convolution = np.convolve(poly1, poly2)
    # return np.dot(convolution, moments[:len(convolution)])
    convolution = [mpf(0)] * (len(poly1) + len(poly2) - 1)
    for i in range(len(poly1)):
        for j in range(len(poly2)):
            convolution[i + j] += poly1[i] * poly2[j]
    return sum(
        c * m
        for c, m in zip(convolution, moments[: len(convolution)], strict=False)
    )

def get_coef_alpha_beta_recursive(n_order, moments):
    # monic_coefs = [[1.0]]
    monic_coefs = [[mpf(1)]]
    alpha = []
    beta = []
    norm = []  # <pi_k,pi_k>
    for n in range(n_order):
        # coefs_pi_k = [0.0] + monic_coefs[-1]
        coefs_pi_k = [mpf(0)] + monic_coefs[-1]
        # coefs_x_pi_k = monic_coefs[-1] + [0.0]
        coefs_x_pi_k = monic_coefs[-1] + [mpf(0)]
        assert coefs_x_pi_k[0] == 1.0
        # <pi_k,pi_k>
        alpha_denom = polynomial_inner_product(
            np.array(coefs_pi_k)[::-1],
            np.array(coefs_pi_k)[::-1],
            np.array(moments),
        )
        # <x pi_k,pi_k>
        alpha_num = polynomial_inner_product(
            np.array(coefs_x_pi_k)[::-1],
            np.array(coefs_pi_k)[::-1],
            np.array(moments),
        )
        alpha.append(alpha_num / alpha_denom)
        norm.append(alpha_denom)
        if n >= 1:
            beta_num = norm[-1]
            beta_denom = norm[-2]
            beta.append(beta_num / beta_denom)
        else:
            # beta.append(0.0)
            beta.append(mpf(0))
        monic_coefs.append(coefs_x_pi_k)
        for i in range(len(monic_coefs[-2])):
            monic_coefs[-1][-i - 1] -= alpha[-1] * monic_coefs[-2][-i - 1]
        if n >= 1:
            for i in range(len(monic_coefs[-3])):
                monic_coefs[-1][-i - 1] -= beta[-1] * monic_coefs[-3][-i - 1]
    return monic_coefs, alpha, beta, norm


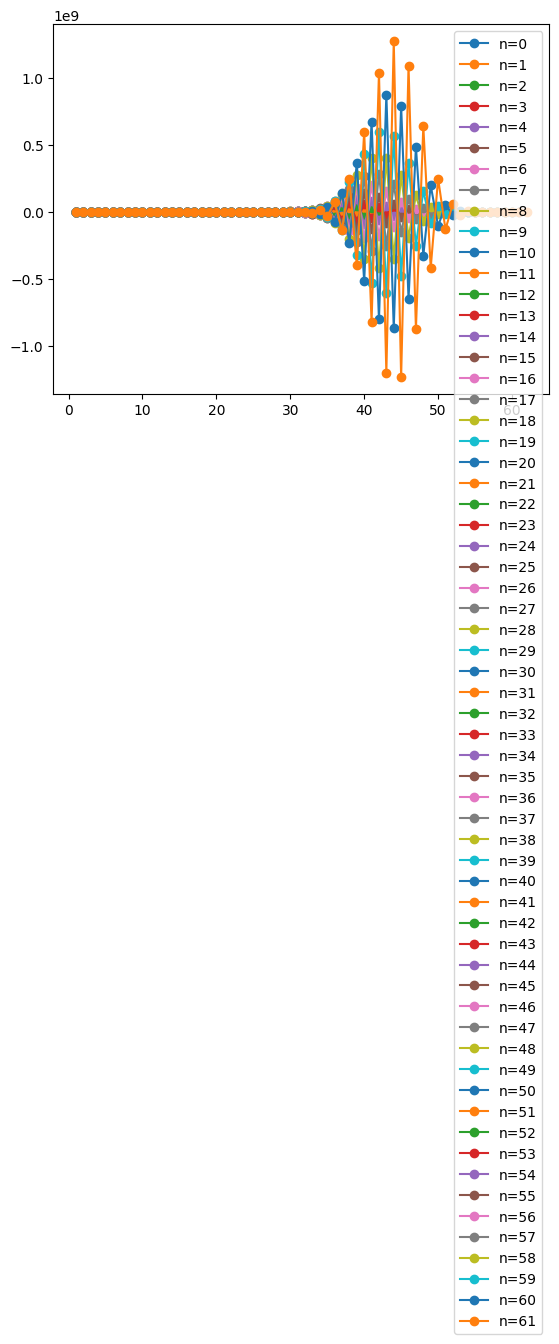
monic_coefs, alpha, beta, norm = get_coef_alpha_beta_recursive(n_order, moments)

for i in range(len(monic_coefs)):
    plt.plot(
        np.arange(i + 1, 0, -1), monic_coefs[i], label=f"n={i}", marker="o"
    )
plt.legend()
plt.show()

plt.plot(alpha, label="alpha")
plt.plot(beta, label="beta")
plt.legend()
plt.show()

plt.plot(norm, label="norm")
plt.legend()
plt.show()

plt.plot(np.abs(np.array(alpha) - 1 / 2) * L, label="L|alpha-1/2|", marker="o")
plt.plot(
    np.abs(1 / 16 - np.array(beta)) * L * L, label="L^2|1/16-beta|", marker="x"
)
plt.yscale("log")
plt.legend()
plt.show()

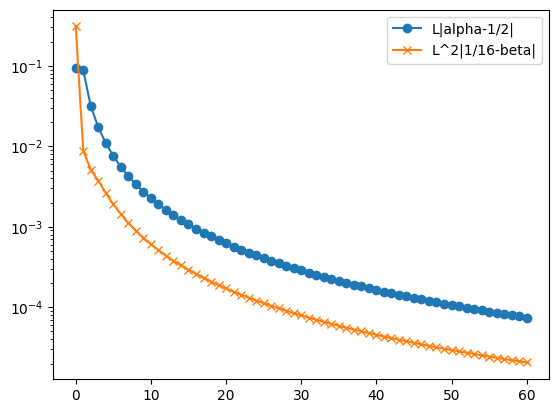
Then, we have the parameters

\[c_0 = |\pi_0| = \sqrt{m_0} = \sqrt{\frac{1}{2} \log(1+L^2)}\]

\[\omega_n = \omega_{\text{max}} \alpha_n\]

\[t_n = \omega_{\text{max}} \sqrt{\beta_{n+1}}\]

And total Hamiltonian is

\[H_{\text{sys}} + \sqrt{\frac{\lambda\omega_c\log(1+L^2)}{\pi}} \hat{A} (b_0 + b_0^\dagger) + \sum_{n=0}^N \omega_{\text{max}}(\alpha_n b_n^\dagger b_n + \sqrt{\beta_{n+1}} b_{n+1}^\dagger b_n + \sqrt{\beta_{n+1}} b_n^\dagger b_{n+1})\]

where \(\hat{A}\) is the operator like \(\sum_{k} |k\rangle \langle k|\) acting on the electronic state.

backend = "numpy"  # "jax"
c0 = math.sqrt(λ * ωc * math.log(1 + L**2) / math.pi) / units.au_in_eV
omega = np.array(alpha, dtype=np.float64) * ωmax / units.au_in_eV
t = np.sqrt(np.array(beta[1:], dtype=np.float64)) * ωmax / units.au_in_eV

c0_sym = sympy.Symbol("c_0")
omega_syms = [sympy.Symbol(f"omega_{i}") for i in range(len(omega))]
t_syms = [sympy.Symbol(f"t_{i}") for i in range(len(t))]

subs = {}
subs[c0_sym] = c0
for omega_val, omega_sym in zip(omega, omega_syms, strict=True):
    subs[omega_sym] = omega_val
for t_val, t_sym in zip(t, t_syms, strict=True):
    subs[t_sym] = t_val

Setup basis for wavefunction

basis = (
    [Boson(8)] * n_order
    + [Exciton(nstate=3, names=["S1", "TT", "CS"])]
    + [Boson(8)] * (2 * n_order)
)
basinfo = BasInfo([basis])
ndim = len(basis)
print(ndim)
sys_site = n_order

184

Setup one particle operator

eham = (
    np.array([[0.2, 0.0, -0.05], [0.0, 0.0, -0.05], [-0.05, -0.05, 0.3]])
    / units.au_in_eV
)
b = basis[0].get_annihilation_matrix()
bdag = basis[0].get_creation_matrix()
num = basis[0].get_number_matrix()
bdagb = num

s1 = np.zeros((3, 3))
s1[0, 0] = 1.0  # act only on S1

tt = np.zeros((3, 3))
tt[1, 1] = 1.0  # act only on TT

ct = np.zeros((3, 3))
ct[2, 2] = 1.0  # act only on CT

eham_op = OpSite("H_{" + f"{sys_site}" + "}", sys_site, value=eham)
s1_op = OpSite("S1" + "_{" + f"{sys_site}" + "}", sys_site, value=s1)
tt_op = OpSite(r"\text{TT}" + "_{" + f"{sys_site}" + "}", sys_site, value=tt)
ct_op = OpSite(r"\text{CT}" + "_{" + f"{sys_site}" + "}", sys_site, value=ct)

b_ops = [
    OpSite("b_{" + f"{n}" + "}", n, value=b) if n != sys_site else None
    for n in range(3 * n_order + 1)
]
bdag_ops = [
    OpSite(r"b^\dagger" + "_{" + f"{n}" + "}", n, value=bdag)
    if n != sys_site
    else None
    for n in range(3 * n_order + 1)
]
bdagb_ops = [
    OpSite(
        r"b^\dagger" + "_{" + f"{n}" + "}" + "b_{" + f"{n}" + "}",
        n,
        value=bdagb,
    )
    if n != sys_site
    else None
    for n in range(3 * n_order + 1)
]

Setup potential and kinetic operator

sop = SumOfProducts()
sop += eham_op

sop += c0_sym * s1_op * (b_ops[sys_site - 1] + bdag_ops[sys_site - 1])
for i, n in enumerate(range(sys_site - 1, -1, -1)):
    sop += omega_syms[i] * bdagb_ops[n]
    if i != n_order - 1:
        sop += t_syms[i] * (
            b_ops[n] * bdag_ops[n - 1] + bdag_ops[n] * b_ops[n - 1]
        )

sop += c0_sym * ct_op * (b_ops[sys_site + 1] + bdag_ops[sys_site + 1])
for i, n in enumerate(range(sys_site + 1, 3 * n_order, 2)):
    sop += omega_syms[i] * bdagb_ops[n]
    if i != n_order - 1:
        sop += t_syms[i] * (
            b_ops[n] * bdag_ops[n + 1] + bdag_ops[n] * b_ops[n + 1]
        )

sop += c0_sym * tt_op * (b_ops[sys_site + 2] + bdag_ops[sys_site + 2])
for i, n in enumerate(range(sys_site + 2, 3 * n_order + 1, 2)):
    sop += omega_syms[i] * bdagb_ops[n]
    if i != n_order - 1:
        sop += t_syms[i] * (
            b_ops[n] * bdag_ops[n + 1] + bdag_ops[n] * b_ops[n + 1]
        )

sop = sop.simplify()
sop.symbol

$\displaystyle c_{0} \text{CT}_{61} \left(b^\dagger_{62} + b_{62}\right) + c_{0} \text{TT}_{61} \left(b^\dagger_{63} + b_{63}\right) + c_{0} \left(b^\dagger_{60} + b_{60}\right) S1_{61} + \omega_{0} b^\dagger_{60}b_{60} + \omega_{0} b^\dagger_{62}b_{62} + \omega_{0} b^\dagger_{63}b_{63} + \omega_{1} b^\dagger_{59}b_{59} + \omega_{1} b^\dagger_{64}b_{64} + \omega_{1} b^\dagger_{65}b_{65} + \omega_{10} b^\dagger_{50}b_{50} + \omega_{10} b^\dagger_{82}b_{82} + \omega_{10} b^\dagger_{83}b_{83} + \omega_{11} b^\dagger_{49}b_{49} + \omega_{11} b^\dagger_{84}b_{84} + \omega_{11} b^\dagger_{85}b_{85} + \omega_{12} b^\dagger_{48}b_{48} + \omega_{12} b^\dagger_{86}b_{86} + \omega_{12} b^\dagger_{87}b_{87} + \omega_{13} b^\dagger_{47}b_{47} + \omega_{13} b^\dagger_{88}b_{88} + \omega_{13} b^\dagger_{89}b_{89} + \omega_{14} b^\dagger_{46}b_{46} + \omega_{14} b^\dagger_{90}b_{90} + \omega_{14} b^\dagger_{91}b_{91} + \omega_{15} b^\dagger_{45}b_{45} + \omega_{15} b^\dagger_{92}b_{92} + \omega_{15} b^\dagger_{93}b_{93} + \omega_{16} b^\dagger_{44}b_{44} + \omega_{16} b^\dagger_{94}b_{94} + \omega_{16} b^\dagger_{95}b_{95} + \omega_{17} b^\dagger_{43}b_{43} + \omega_{17} b^\dagger_{96}b_{96} + \omega_{17} b^\dagger_{97}b_{97} + \omega_{18} b^\dagger_{42}b_{42} + \omega_{18} b^\dagger_{98}b_{98} + \omega_{18} b^\dagger_{99}b_{99} + \omega_{19} b^\dagger_{100}b_{100} + \omega_{19} b^\dagger_{101}b_{101} + \omega_{19} b^\dagger_{41}b_{41} + \omega_{2} b^\dagger_{58}b_{58} + \omega_{2} b^\dagger_{66}b_{66} + \omega_{2} b^\dagger_{67}b_{67} + \omega_{20} b^\dagger_{102}b_{102} + \omega_{20} b^\dagger_{103}b_{103} + \omega_{20} b^\dagger_{40}b_{40} + \omega_{21} b^\dagger_{104}b_{104} + \omega_{21} b^\dagger_{105}b_{105} + \omega_{21} b^\dagger_{39}b_{39} + \omega_{22} b^\dagger_{106}b_{106} + \omega_{22} b^\dagger_{107}b_{107} + \omega_{22} b^\dagger_{38}b_{38} + \omega_{23} b^\dagger_{108}b_{108} + \omega_{23} b^\dagger_{109}b_{109} + \omega_{23} b^\dagger_{37}b_{37} + \omega_{24} b^\dagger_{110}b_{110} + \omega_{24} b^\dagger_{111}b_{111} + \omega_{24} b^\dagger_{36}b_{36} + \omega_{25} b^\dagger_{112}b_{112} + \omega_{25} b^\dagger_{113}b_{113} + \omega_{25} b^\dagger_{35}b_{35} + \omega_{26} b^\dagger_{114}b_{114} + \omega_{26} b^\dagger_{115}b_{115} + \omega_{26} b^\dagger_{34}b_{34} + \omega_{27} b^\dagger_{116}b_{116} + \omega_{27} b^\dagger_{117}b_{117} + \omega_{27} b^\dagger_{33}b_{33} + \omega_{28} b^\dagger_{118}b_{118} + \omega_{28} b^\dagger_{119}b_{119} + \omega_{28} b^\dagger_{32}b_{32} + \omega_{29} b^\dagger_{120}b_{120} + \omega_{29} b^\dagger_{121}b_{121} + \omega_{29} b^\dagger_{31}b_{31} + \omega_{3} b^\dagger_{57}b_{57} + \omega_{3} b^\dagger_{68}b_{68} + \omega_{3} b^\dagger_{69}b_{69} + \omega_{30} b^\dagger_{122}b_{122} + \omega_{30} b^\dagger_{123}b_{123} + \omega_{30} b^\dagger_{30}b_{30} + \omega_{31} b^\dagger_{124}b_{124} + \omega_{31} b^\dagger_{125}b_{125} + \omega_{31} b^\dagger_{29}b_{29} + \omega_{32} b^\dagger_{126}b_{126} + \omega_{32} b^\dagger_{127}b_{127} + \omega_{32} b^\dagger_{28}b_{28} + \omega_{33} b^\dagger_{128}b_{128} + \omega_{33} b^\dagger_{129}b_{129} + \omega_{33} b^\dagger_{27}b_{27} + \omega_{34} b^\dagger_{130}b_{130} + \omega_{34} b^\dagger_{131}b_{131} + \omega_{34} b^\dagger_{26}b_{26} + \omega_{35} b^\dagger_{132}b_{132} + \omega_{35} b^\dagger_{133}b_{133} + \omega_{35} b^\dagger_{25}b_{25} + \omega_{36} b^\dagger_{134}b_{134} + \omega_{36} b^\dagger_{135}b_{135} + \omega_{36} b^\dagger_{24}b_{24} + \omega_{37} b^\dagger_{136}b_{136} + \omega_{37} b^\dagger_{137}b_{137} + \omega_{37} b^\dagger_{23}b_{23} + \omega_{38} b^\dagger_{138}b_{138} + \omega_{38} b^\dagger_{139}b_{139} + \omega_{38} b^\dagger_{22}b_{22} + \omega_{39} b^\dagger_{140}b_{140} + \omega_{39} b^\dagger_{141}b_{141} + \omega_{39} b^\dagger_{21}b_{21} + \omega_{4} b^\dagger_{56}b_{56} + \omega_{4} b^\dagger_{70}b_{70} + \omega_{4} b^\dagger_{71}b_{71} + \omega_{40} b^\dagger_{142}b_{142} + \omega_{40} b^\dagger_{143}b_{143} + \omega_{40} b^\dagger_{20}b_{20} + \omega_{41} b^\dagger_{144}b_{144} + \omega_{41} b^\dagger_{145}b_{145} + \omega_{41} b^\dagger_{19}b_{19} + \omega_{42} b^\dagger_{146}b_{146} + \omega_{42} b^\dagger_{147}b_{147} + \omega_{42} b^\dagger_{18}b_{18} + \omega_{43} b^\dagger_{148}b_{148} + \omega_{43} b^\dagger_{149}b_{149} + \omega_{43} b^\dagger_{17}b_{17} + \omega_{44} b^\dagger_{150}b_{150} + \omega_{44} b^\dagger_{151}b_{151} + \omega_{44} b^\dagger_{16}b_{16} + \omega_{45} b^\dagger_{152}b_{152} + \omega_{45} b^\dagger_{153}b_{153} + \omega_{45} b^\dagger_{15}b_{15} + \omega_{46} b^\dagger_{14}b_{14} + \omega_{46} b^\dagger_{154}b_{154} + \omega_{46} b^\dagger_{155}b_{155} + \omega_{47} b^\dagger_{13}b_{13} + \omega_{47} b^\dagger_{156}b_{156} + \omega_{47} b^\dagger_{157}b_{157} + \omega_{48} b^\dagger_{12}b_{12} + \omega_{48} b^\dagger_{158}b_{158} + \omega_{48} b^\dagger_{159}b_{159} + \omega_{49} b^\dagger_{11}b_{11} + \omega_{49} b^\dagger_{160}b_{160} + \omega_{49} b^\dagger_{161}b_{161} + \omega_{5} b^\dagger_{55}b_{55} + \omega_{5} b^\dagger_{72}b_{72} + \omega_{5} b^\dagger_{73}b_{73} + \omega_{50} b^\dagger_{10}b_{10} + \omega_{50} b^\dagger_{162}b_{162} + \omega_{50} b^\dagger_{163}b_{163} + \omega_{51} b^\dagger_{164}b_{164} + \omega_{51} b^\dagger_{165}b_{165} + \omega_{51} b^\dagger_{9}b_{9} + \omega_{52} b^\dagger_{166}b_{166} + \omega_{52} b^\dagger_{167}b_{167} + \omega_{52} b^\dagger_{8}b_{8} + \omega_{53} b^\dagger_{168}b_{168} + \omega_{53} b^\dagger_{169}b_{169} + \omega_{53} b^\dagger_{7}b_{7} + \omega_{54} b^\dagger_{170}b_{170} + \omega_{54} b^\dagger_{171}b_{171} + \omega_{54} b^\dagger_{6}b_{6} + \omega_{55} b^\dagger_{172}b_{172} + \omega_{55} b^\dagger_{173}b_{173} + \omega_{55} b^\dagger_{5}b_{5} + \omega_{56} b^\dagger_{174}b_{174} + \omega_{56} b^\dagger_{175}b_{175} + \omega_{56} b^\dagger_{4}b_{4} + \omega_{57} b^\dagger_{176}b_{176} + \omega_{57} b^\dagger_{177}b_{177} + \omega_{57} b^\dagger_{3}b_{3} + \omega_{58} b^\dagger_{178}b_{178} + \omega_{58} b^\dagger_{179}b_{179} + \omega_{58} b^\dagger_{2}b_{2} + \omega_{59} b^\dagger_{180}b_{180} + \omega_{59} b^\dagger_{181}b_{181} + \omega_{59} b^\dagger_{1}b_{1} + \omega_{6} b^\dagger_{54}b_{54} + \omega_{6} b^\dagger_{74}b_{74} + \omega_{6} b^\dagger_{75}b_{75} + \omega_{60} b^\dagger_{0}b_{0} + \omega_{60} b^\dagger_{182}b_{182} + \omega_{60} b^\dagger_{183}b_{183} + \omega_{7} b^\dagger_{53}b_{53} + \omega_{7} b^\dagger_{76}b_{76} + \omega_{7} b^\dagger_{77}b_{77} + \omega_{8} b^\dagger_{52}b_{52} + \omega_{8} b^\dagger_{78}b_{78} + \omega_{8} b^\dagger_{79}b_{79} + \omega_{9} b^\dagger_{51}b_{51} + \omega_{9} b^\dagger_{80}b_{80} + \omega_{9} b^\dagger_{81}b_{81} + t_{0} b^\dagger_{59} b_{60} + t_{0} b^\dagger_{62} b_{63} + t_{0} b^\dagger_{63} b_{64} + t_{0} b_{59} b^\dagger_{60} + t_{0} b_{62} b^\dagger_{63} + t_{0} b_{63} b^\dagger_{64} + t_{1} b^\dagger_{58} b_{59} + t_{1} b^\dagger_{64} b_{65} + t_{1} b^\dagger_{65} b_{66} + t_{1} b_{58} b^\dagger_{59} + t_{1} b_{64} b^\dagger_{65} + t_{1} b_{65} b^\dagger_{66} + t_{10} b^\dagger_{49} b_{50} + t_{10} b^\dagger_{82} b_{83} + t_{10} b^\dagger_{83} b_{84} + t_{10} b_{49} b^\dagger_{50} + t_{10} b_{82} b^\dagger_{83} + t_{10} b_{83} b^\dagger_{84} + t_{11} b^\dagger_{48} b_{49} + t_{11} b^\dagger_{84} b_{85} + t_{11} b^\dagger_{85} b_{86} + t_{11} b_{48} b^\dagger_{49} + t_{11} b_{84} b^\dagger_{85} + t_{11} b_{85} b^\dagger_{86} + t_{12} b^\dagger_{47} b_{48} + t_{12} b^\dagger_{86} b_{87} + t_{12} b^\dagger_{87} b_{88} + t_{12} b_{47} b^\dagger_{48} + t_{12} b_{86} b^\dagger_{87} + t_{12} b_{87} b^\dagger_{88} + t_{13} b^\dagger_{46} b_{47} + t_{13} b^\dagger_{88} b_{89} + t_{13} b^\dagger_{89} b_{90} + t_{13} b_{46} b^\dagger_{47} + t_{13} b_{88} b^\dagger_{89} + t_{13} b_{89} b^\dagger_{90} + t_{14} b^\dagger_{45} b_{46} + t_{14} b^\dagger_{90} b_{91} + t_{14} b^\dagger_{91} b_{92} + t_{14} b_{45} b^\dagger_{46} + t_{14} b_{90} b^\dagger_{91} + t_{14} b_{91} b^\dagger_{92} + t_{15} b^\dagger_{44} b_{45} + t_{15} b^\dagger_{92} b_{93} + t_{15} b^\dagger_{93} b_{94} + t_{15} b_{44} b^\dagger_{45} + t_{15} b_{92} b^\dagger_{93} + t_{15} b_{93} b^\dagger_{94} + t_{16} b^\dagger_{43} b_{44} + t_{16} b^\dagger_{94} b_{95} + t_{16} b^\dagger_{95} b_{96} + t_{16} b_{43} b^\dagger_{44} + t_{16} b_{94} b^\dagger_{95} + t_{16} b_{95} b^\dagger_{96} + t_{17} b^\dagger_{42} b_{43} + t_{17} b^\dagger_{96} b_{97} + t_{17} b^\dagger_{97} b_{98} + t_{17} b_{42} b^\dagger_{43} + t_{17} b_{96} b^\dagger_{97} + t_{17} b_{97} b^\dagger_{98} + t_{18} b^\dagger_{41} b_{42} + t_{18} b^\dagger_{98} b_{99} + t_{18} b^\dagger_{99} b_{100} + t_{18} b_{41} b^\dagger_{42} + t_{18} b_{98} b^\dagger_{99} + t_{18} b_{99} b^\dagger_{100} + t_{19} b^\dagger_{100} b_{101} + t_{19} b^\dagger_{101} b_{102} + t_{19} b^\dagger_{40} b_{41} + t_{19} b_{100} b^\dagger_{101} + t_{19} b_{101} b^\dagger_{102} + t_{19} b_{40} b^\dagger_{41} + t_{2} b^\dagger_{57} b_{58} + t_{2} b^\dagger_{66} b_{67} + t_{2} b^\dagger_{67} b_{68} + t_{2} b_{57} b^\dagger_{58} + t_{2} b_{66} b^\dagger_{67} + t_{2} b_{67} b^\dagger_{68} + t_{20} b^\dagger_{102} b_{103} + t_{20} b^\dagger_{103} b_{104} + t_{20} b^\dagger_{39} b_{40} + t_{20} b_{102} b^\dagger_{103} + t_{20} b_{103} b^\dagger_{104} + t_{20} b_{39} b^\dagger_{40} + t_{21} b^\dagger_{104} b_{105} + t_{21} b^\dagger_{105} b_{106} + t_{21} b^\dagger_{38} b_{39} + t_{21} b_{104} b^\dagger_{105} + t_{21} b_{105} b^\dagger_{106} + t_{21} b_{38} b^\dagger_{39} + t_{22} b^\dagger_{106} b_{107} + t_{22} b^\dagger_{107} b_{108} + t_{22} b^\dagger_{37} b_{38} + t_{22} b_{106} b^\dagger_{107} + t_{22} b_{107} b^\dagger_{108} + t_{22} b_{37} b^\dagger_{38} + t_{23} b^\dagger_{108} b_{109} + t_{23} b^\dagger_{109} b_{110} + t_{23} b^\dagger_{36} b_{37} + t_{23} b_{108} b^\dagger_{109} + t_{23} b_{109} b^\dagger_{110} + t_{23} b_{36} b^\dagger_{37} + t_{24} b^\dagger_{110} b_{111} + t_{24} b^\dagger_{111} b_{112} + t_{24} b^\dagger_{35} b_{36} + t_{24} b_{110} b^\dagger_{111} + t_{24} b_{111} b^\dagger_{112} + t_{24} b_{35} b^\dagger_{36} + t_{25} b^\dagger_{112} b_{113} + t_{25} b^\dagger_{113} b_{114} + t_{25} b^\dagger_{34} b_{35} + t_{25} b_{112} b^\dagger_{113} + t_{25} b_{113} b^\dagger_{114} + t_{25} b_{34} b^\dagger_{35} + t_{26} b^\dagger_{114} b_{115} + t_{26} b^\dagger_{115} b_{116} + t_{26} b^\dagger_{33} b_{34} + t_{26} b_{114} b^\dagger_{115} + t_{26} b_{115} b^\dagger_{116} + t_{26} b_{33} b^\dagger_{34} + t_{27} b^\dagger_{116} b_{117} + t_{27} b^\dagger_{117} b_{118} + t_{27} b^\dagger_{32} b_{33} + t_{27} b_{116} b^\dagger_{117} + t_{27} b_{117} b^\dagger_{118} + t_{27} b_{32} b^\dagger_{33} + t_{28} b^\dagger_{118} b_{119} + t_{28} b^\dagger_{119} b_{120} + t_{28} b^\dagger_{31} b_{32} + t_{28} b_{118} b^\dagger_{119} + t_{28} b_{119} b^\dagger_{120} + t_{28} b_{31} b^\dagger_{32} + t_{29} b^\dagger_{120} b_{121} + t_{29} b^\dagger_{121} b_{122} + t_{29} b^\dagger_{30} b_{31} + t_{29} b_{120} b^\dagger_{121} + t_{29} b_{121} b^\dagger_{122} + t_{29} b_{30} b^\dagger_{31} + t_{3} b^\dagger_{56} b_{57} + t_{3} b^\dagger_{68} b_{69} + t_{3} b^\dagger_{69} b_{70} + t_{3} b_{56} b^\dagger_{57} + t_{3} b_{68} b^\dagger_{69} + t_{3} b_{69} b^\dagger_{70} + t_{30} b^\dagger_{122} b_{123} + t_{30} b^\dagger_{123} b_{124} + t_{30} b^\dagger_{29} b_{30} + t_{30} b_{122} b^\dagger_{123} + t_{30} b_{123} b^\dagger_{124} + t_{30} b_{29} b^\dagger_{30} + t_{31} b^\dagger_{124} b_{125} + t_{31} b^\dagger_{125} b_{126} + t_{31} b^\dagger_{28} b_{29} + t_{31} b_{124} b^\dagger_{125} + t_{31} b_{125} b^\dagger_{126} + t_{31} b_{28} b^\dagger_{29} + t_{32} b^\dagger_{126} b_{127} + t_{32} b^\dagger_{127} b_{128} + t_{32} b^\dagger_{27} b_{28} + t_{32} b_{126} b^\dagger_{127} + t_{32} b_{127} b^\dagger_{128} + t_{32} b_{27} b^\dagger_{28} + t_{33} b^\dagger_{128} b_{129} + t_{33} b^\dagger_{129} b_{130} + t_{33} b^\dagger_{26} b_{27} + t_{33} b_{128} b^\dagger_{129} + t_{33} b_{129} b^\dagger_{130} + t_{33} b_{26} b^\dagger_{27} + t_{34} b^\dagger_{130} b_{131} + t_{34} b^\dagger_{131} b_{132} + t_{34} b^\dagger_{25} b_{26} + t_{34} b_{130} b^\dagger_{131} + t_{34} b_{131} b^\dagger_{132} + t_{34} b_{25} b^\dagger_{26} + t_{35} b^\dagger_{132} b_{133} + t_{35} b^\dagger_{133} b_{134} + t_{35} b^\dagger_{24} b_{25} + t_{35} b_{132} b^\dagger_{133} + t_{35} b_{133} b^\dagger_{134} + t_{35} b_{24} b^\dagger_{25} + t_{36} b^\dagger_{134} b_{135} + t_{36} b^\dagger_{135} b_{136} + t_{36} b^\dagger_{23} b_{24} + t_{36} b_{134} b^\dagger_{135} + t_{36} b_{135} b^\dagger_{136} + t_{36} b_{23} b^\dagger_{24} + t_{37} b^\dagger_{136} b_{137} + t_{37} b^\dagger_{137} b_{138} + t_{37} b^\dagger_{22} b_{23} + t_{37} b_{136} b^\dagger_{137} + t_{37} b_{137} b^\dagger_{138} + t_{37} b_{22} b^\dagger_{23} + t_{38} b^\dagger_{138} b_{139} + t_{38} b^\dagger_{139} b_{140} + t_{38} b^\dagger_{21} b_{22} + t_{38} b_{138} b^\dagger_{139} + t_{38} b_{139} b^\dagger_{140} + t_{38} b_{21} b^\dagger_{22} + t_{39} b^\dagger_{140} b_{141} + t_{39} b^\dagger_{141} b_{142} + t_{39} b^\dagger_{20} b_{21} + t_{39} b_{140} b^\dagger_{141} + t_{39} b_{141} b^\dagger_{142} + t_{39} b_{20} b^\dagger_{21} + t_{4} b^\dagger_{55} b_{56} + t_{4} b^\dagger_{70} b_{71} + t_{4} b^\dagger_{71} b_{72} + t_{4} b_{55} b^\dagger_{56} + t_{4} b_{70} b^\dagger_{71} + t_{4} b_{71} b^\dagger_{72} + t_{40} b^\dagger_{142} b_{143} + t_{40} b^\dagger_{143} b_{144} + t_{40} b^\dagger_{19} b_{20} + t_{40} b_{142} b^\dagger_{143} + t_{40} b_{143} b^\dagger_{144} + t_{40} b_{19} b^\dagger_{20} + t_{41} b^\dagger_{144} b_{145} + t_{41} b^\dagger_{145} b_{146} + t_{41} b^\dagger_{18} b_{19} + t_{41} b_{144} b^\dagger_{145} + t_{41} b_{145} b^\dagger_{146} + t_{41} b_{18} b^\dagger_{19} + t_{42} b^\dagger_{146} b_{147} + t_{42} b^\dagger_{147} b_{148} + t_{42} b^\dagger_{17} b_{18} + t_{42} b_{146} b^\dagger_{147} + t_{42} b_{147} b^\dagger_{148} + t_{42} b_{17} b^\dagger_{18} + t_{43} b^\dagger_{148} b_{149} + t_{43} b^\dagger_{149} b_{150} + t_{43} b^\dagger_{16} b_{17} + t_{43} b_{148} b^\dagger_{149} + t_{43} b_{149} b^\dagger_{150} + t_{43} b_{16} b^\dagger_{17} + t_{44} b^\dagger_{150} b_{151} + t_{44} b^\dagger_{151} b_{152} + t_{44} b^\dagger_{15} b_{16} + t_{44} b_{150} b^\dagger_{151} + t_{44} b_{151} b^\dagger_{152} + t_{44} b_{15} b^\dagger_{16} + t_{45} b^\dagger_{14} b_{15} + t_{45} b^\dagger_{152} b_{153} + t_{45} b^\dagger_{153} b_{154} + t_{45} b_{14} b^\dagger_{15} + t_{45} b_{152} b^\dagger_{153} + t_{45} b_{153} b^\dagger_{154} + t_{46} b^\dagger_{13} b_{14} + t_{46} b^\dagger_{154} b_{155} + t_{46} b^\dagger_{155} b_{156} + t_{46} b_{13} b^\dagger_{14} + t_{46} b_{154} b^\dagger_{155} + t_{46} b_{155} b^\dagger_{156} + t_{47} b^\dagger_{12} b_{13} + t_{47} b^\dagger_{156} b_{157} + t_{47} b^\dagger_{157} b_{158} + t_{47} b_{12} b^\dagger_{13} + t_{47} b_{156} b^\dagger_{157} + t_{47} b_{157} b^\dagger_{158} + t_{48} b^\dagger_{11} b_{12} + t_{48} b^\dagger_{158} b_{159} + t_{48} b^\dagger_{159} b_{160} + t_{48} b_{11} b^\dagger_{12} + t_{48} b_{158} b^\dagger_{159} + t_{48} b_{159} b^\dagger_{160} + t_{49} b^\dagger_{10} b_{11} + t_{49} b^\dagger_{160} b_{161} + t_{49} b^\dagger_{161} b_{162} + t_{49} b_{10} b^\dagger_{11} + t_{49} b_{160} b^\dagger_{161} + t_{49} b_{161} b^\dagger_{162} + t_{5} b^\dagger_{54} b_{55} + t_{5} b^\dagger_{72} b_{73} + t_{5} b^\dagger_{73} b_{74} + t_{5} b_{54} b^\dagger_{55} + t_{5} b_{72} b^\dagger_{73} + t_{5} b_{73} b^\dagger_{74} + t_{50} b^\dagger_{162} b_{163} + t_{50} b^\dagger_{163} b_{164} + t_{50} b^\dagger_{9} b_{10} + t_{50} b_{162} b^\dagger_{163} + t_{50} b_{163} b^\dagger_{164} + t_{50} b_{9} b^\dagger_{10} + t_{51} b^\dagger_{164} b_{165} + t_{51} b^\dagger_{165} b_{166} + t_{51} b^\dagger_{8} b_{9} + t_{51} b_{164} b^\dagger_{165} + t_{51} b_{165} b^\dagger_{166} + t_{51} b_{8} b^\dagger_{9} + t_{52} b^\dagger_{166} b_{167} + t_{52} b^\dagger_{167} b_{168} + t_{52} b^\dagger_{7} b_{8} + t_{52} b_{166} b^\dagger_{167} + t_{52} b_{167} b^\dagger_{168} + t_{52} b_{7} b^\dagger_{8} + t_{53} b^\dagger_{168} b_{169} + t_{53} b^\dagger_{169} b_{170} + t_{53} b^\dagger_{6} b_{7} + t_{53} b_{168} b^\dagger_{169} + t_{53} b_{169} b^\dagger_{170} + t_{53} b_{6} b^\dagger_{7} + t_{54} b^\dagger_{170} b_{171} + t_{54} b^\dagger_{171} b_{172} + t_{54} b^\dagger_{5} b_{6} + t_{54} b_{170} b^\dagger_{171} + t_{54} b_{171} b^\dagger_{172} + t_{54} b_{5} b^\dagger_{6} + t_{55} b^\dagger_{172} b_{173} + t_{55} b^\dagger_{173} b_{174} + t_{55} b^\dagger_{4} b_{5} + t_{55} b_{172} b^\dagger_{173} + t_{55} b_{173} b^\dagger_{174} + t_{55} b_{4} b^\dagger_{5} + t_{56} b^\dagger_{174} b_{175} + t_{56} b^\dagger_{175} b_{176} + t_{56} b^\dagger_{3} b_{4} + t_{56} b_{174} b^\dagger_{175} + t_{56} b_{175} b^\dagger_{176} + t_{56} b_{3} b^\dagger_{4} + t_{57} b^\dagger_{176} b_{177} + t_{57} b^\dagger_{177} b_{178} + t_{57} b^\dagger_{2} b_{3} + t_{57} b_{176} b^\dagger_{177} + t_{57} b_{177} b^\dagger_{178} + t_{57} b_{2} b^\dagger_{3} + t_{58} b^\dagger_{178} b_{179} + t_{58} b^\dagger_{179} b_{180} + t_{58} b^\dagger_{1} b_{2} + t_{58} b_{178} b^\dagger_{179} + t_{58} b_{179} b^\dagger_{180} + t_{58} b_{1} b^\dagger_{2} + t_{59} b^\dagger_{0} b_{1} + t_{59} b^\dagger_{180} b_{181} + t_{59} b^\dagger_{181} b_{182} + t_{59} b_{0} b^\dagger_{1} + t_{59} b_{180} b^\dagger_{181} + t_{59} b_{181} b^\dagger_{182} + t_{6} b^\dagger_{53} b_{54} + t_{6} b^\dagger_{74} b_{75} + t_{6} b^\dagger_{75} b_{76} + t_{6} b_{53} b^\dagger_{54} + t_{6} b_{74} b^\dagger_{75} + t_{6} b_{75} b^\dagger_{76} + t_{7} b^\dagger_{52} b_{53} + t_{7} b^\dagger_{76} b_{77} + t_{7} b^\dagger_{77} b_{78} + t_{7} b_{52} b^\dagger_{53} + t_{7} b_{76} b^\dagger_{77} + t_{7} b_{77} b^\dagger_{78} + t_{8} b^\dagger_{51} b_{52} + t_{8} b^\dagger_{78} b_{79} + t_{8} b^\dagger_{79} b_{80} + t_{8} b_{51} b^\dagger_{52} + t_{8} b_{78} b^\dagger_{79} + t_{8} b_{79} b^\dagger_{80} + t_{9} b^\dagger_{50} b_{51} + t_{9} b^\dagger_{80} b_{81} + t_{9} b^\dagger_{81} b_{82} + t_{9} b_{50} b^\dagger_{51} + t_{9} b_{80} b^\dagger_{81} + t_{9} b_{81} b^\dagger_{82} + H_{61}$

Setup MPO

am_pot = AssignManager(sop)
am_pot.assign()
W_prod = sympy.Mul(*am_pot.Wsym)
assert W_prod[0] == sop.symbol, W_prod[0] - sop.symbol
pot_mpo = am_pot.numerical_mpo(subs=subs)
export_npz(pot_mpo, "singlet_fission_mpo.npz")
# display(*am_pot.Wsym)

Setup Hamiltonian

# MPO has legs on (0,1,2, ... ,f-1) sites. This legs are given by tuple key
potential = [
    [{tuple((k, k) for k in range(ndim)): TensorOperator(mpo=pot_mpo)}]
]  # key is ((0,0), 1, 2, ..., ndim-1)

H = TensorHamiltonian(
    ndof=len(basis), potential=potential, kinetic=None, backend=backend
)

core = np.zeros((1, 3, 1))
core[0, 0, 0] = 1.0
s1 = TensorHamiltonian(
    ndof=len(basis),
    potential=[[{(sys_site,): TensorOperator(mpo=[core], legs=(sys_site,))}]],
    kinetic=None,
    backend=backend,
)
operators = {"hamiltonian": H, "S1": s1}

from itertools import chain

sites = chain(
    range(sys_site - 1, -1, -4),
    range(sys_site + 1, 3 * n_order + 1, 8),
    range(sys_site + 2, 3 * n_order + 1, 8),
)
for isite in sites:
    core = np.zeros((1, basis[isite].nprim, 1))
    core[0, :, 0] = np.arange(basis[isite].nprim)
    n = TensorHamiltonian(
        ndof=len(basis),
        potential=[[{(isite,): TensorOperator(mpo=[core], legs=(isite,))}]],
        kinetic=None,
        backend=backend,
    )
    operators[f"N{isite}"] = n

Setup Model (basis, operators, initial states)

model = Model(basinfo=basinfo, operators=operators)
model.m_aux_max = 20
# Starts from S1 state
init_boson = [[1.0] + [0.0] * (basis[1].nprim - 1)]
model.init_HartreeProduct = [
    init_boson * n_order + [[1.0, 0.0, 0.0]] + init_boson * (2 * n_order)
]

Execution

jobname = "singlet_fission"
simulator = Simulator(jobname=jobname, model=model, backend=backend, verbose=2)
simulator.propagate(
    maxstep=2000,
    stepsize=0.2,
    reduced_density=(
        [(sys_site, sys_site)],
        10,
    ),  # we want to know diagonal_element of (|S1><S1| |CT><CT| |TT><TT| |S1><CT| |S1><TT| |CS><TT|)
    energy=False,
    autocorr=False,
    observables=True,
    observables_per_step=10,
)

18:30:09 | INFO | Log file is ./singlet_fission_prop/main.log
18:30:09 | INFO | Wave function is saved in wf_singlet_fission.pkl
18:30:09 | INFO | Start initial step    0.000 [fs]

18:30:11 | INFO | End     0 step; propagated    0.200 [fs]; AVG Krylov iteration: 5.64
18:32:28 | INFO | End   100 step; propagated   20.200 [fs]; AVG Krylov iteration: 5.88
18:34:43 | INFO | End   200 step; propagated   40.200 [fs]; AVG Krylov iteration: 5.53
18:36:58 | INFO | End   300 step; propagated   60.200 [fs]; AVG Krylov iteration: 5.62
18:39:07 | INFO | End   400 step; propagated   80.200 [fs]; AVG Krylov iteration: 5.41
18:41:08 | INFO | End   500 step; propagated  100.200 [fs]; AVG Krylov iteration: 5.10
18:43:09 | INFO | End   600 step; propagated  120.200 [fs]; AVG Krylov iteration: 5.07
18:45:08 | INFO | End   700 step; propagated  140.200 [fs]; AVG Krylov iteration: 5.22
18:47:08 | INFO | End   800 step; propagated  160.200 [fs]; AVG Krylov iteration: 5.29
18:49:07 | INFO | End   900 step; propagated  180.200 [fs]; AVG Krylov iteration: 5.24
18:51:05 | INFO | Saved wavefunction  199.800 [fs]
18:51:08 | INFO | End  1000 step; propagated  200.200 [fs]; AVG Krylov iteration: 5.23
18:53:09 | INFO | End  1100 step; propagated  220.200 [fs]; AVG Krylov iteration: 5.19
18:55:10 | INFO | End  1200 step; propagated  240.200 [fs]; AVG Krylov iteration: 5.14
18:57:10 | INFO | End  1300 step; propagated  260.200 [fs]; AVG Krylov iteration: 5.17
18:59:11 | INFO | End  1400 step; propagated  280.200 [fs]; AVG Krylov iteration: 5.17
19:01:10 | INFO | End  1500 step; propagated  300.200 [fs]; AVG Krylov iteration: 5.12
19:03:08 | INFO | End  1600 step; propagated  320.200 [fs]; AVG Krylov iteration: 5.10
19:05:11 | INFO | End  1700 step; propagated  340.200 [fs]; AVG Krylov iteration: 5.06
19:07:08 | INFO | End  1800 step; propagated  360.200 [fs]; AVG Krylov iteration: 5.03
19:09:05 | INFO | End  1900 step; propagated  380.200 [fs]; AVG Krylov iteration: 5.02
19:10:58 | INFO | Saved wavefunction  399.800 [fs]
19:11:00 | INFO | End  1999 step; propagated  399.800 [fs]; AVG Krylov iteration: 5.01
19:11:00 | INFO | End simulation and save wavefunction
19:11:00 | INFO | Wave function is saved in wf_singlet_fission.pkl

(None, <pytdscf.wavefunction.WFunc at 0x131f67230>)

Check results (reduced densities)

import netCDF4 as nc

with nc.Dataset(f"{jobname}_prop/reduced_density.nc", "r") as file:
    density_data_real = file.variables[f"rho_({sys_site}, {sys_site})_0"][:][
        "real"
    ]
    density_data_imag = file.variables[f"rho_({sys_site}, {sys_site})_0"][:][
        "imag"
    ]
    time_data = file.variables["time"][:]

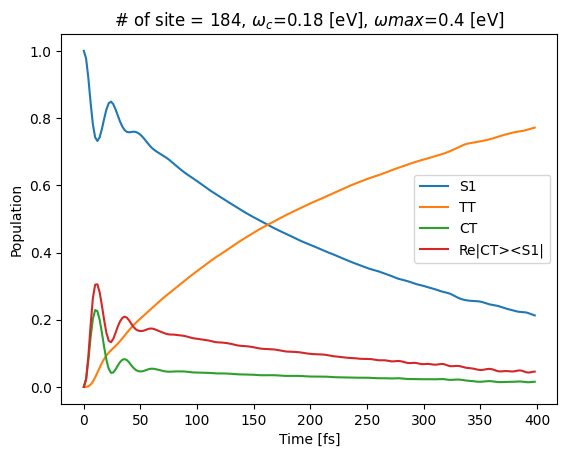
plt.title(f"# of site = {len(basis)}, $ω_c$={ωc} [eV], $ωmax$={ωmax} [eV]")
plt.ylabel("Population")
plt.xlabel("Time [fs]")
plt.plot(time_data, density_data_real[:, 0, 0], label="S1")
plt.plot(time_data, density_data_real[:, 1, 1], label="TT")
plt.plot(time_data, density_data_real[:, 2, 2], label="CT")
plt.plot(time_data, density_data_real[:, 0, 2], label="Re|CT><S1|")
plt.legend()
plt.show()

density_data = np.array(density_data_real) + 1.0j * np.array(density_data_imag)
time_data = np.array(time_data)

from IPython.display import HTML

from pytdscf.util.anim_density_matrix import get_anim

fig, anim = get_anim(
    density_data,
    time_data,
    title="Reduced density matrix",
    time_unit="fs",
    row_names=[r"$|S1\rangle$", r"$|TT\rangle$", r"$|CT\rangle$"],
    col_names=[r"$\langle S1|$", r"$\langle TT|$", r"$\langle CT|$"],
)
HTML(anim.to_jshtml())

Once Loop Reflect

import re

import polars as pl

path = f"{jobname}_prop/expectations.dat"
with open(path, "r") as f:
    header = f.readline().strip()
    columns = re.split(r"\s+", header)
    columns = [columns[1]] + columns[3:]

    data = f.readlines()

df = pl.read_csv(
    path,
    separator="\t",
    new_columns=columns,
    has_header=False,
    skip_rows=1,
    schema_overrides={col: pl.Float64 for col in columns},
)
plt.figure(figsize=(27, 10))
plt.imshow(df[columns[2:]], aspect=5.0e-02)
plt.colorbar()
plt.ylabel("time [fs]")
plt.yticks(np.arange(len(df))[::50], df["time"][::50])
plt.xticks(np.arange(len(columns) - 2), [name[1:] for name in columns[2:]])
plt.title(r"$\langle \hat{N}_i \rangle$")
plt.show()