Example 13 Donor-acceptor relaxation with linear vibronic coupling
This example takes a while. (a couple of hours)
[1]:
import platform
import sys
import pytdscf
print(sys.version)
print(f"pytdscf version = {pytdscf.__version__}")
print(platform.platform())
import jax.extend
print(jax.extend.backend.get_backend().platform)
3.13.2 (main, Feb 4 2025, 14:51:09) [Clang 16.0.0 (clang-1600.0.26.6)]
pytdscf version = 1.1.0
macOS-15.4.1-arm64-arm-64bit-Mach-O
cpu
[2]:
import matplotlib.pyplot as plt
import numpy as np
import sympy
from pympo import AssignManager, OpSite, SumOfProducts
from pytdscf import BasInfo, Boson, Exciton, Model, Simulator, units
from pytdscf.dvr_operator_cls import TensorOperator
from pytdscf.hamiltonian_cls import TensorHamiltonian
Model Hamiltonian
This model contains two electronic states (LE and CS), one intermolecular mode, and 100 effective vibration modes.
\[\begin{split}\begin{align}
H =& \epsilon_{\text{CS}} |\text{CS}\rangle \langle \text{CS}| + t_{\text{LE,CS}} \left[ |\text{CS}\rangle \langle \text{LE}| + |\text{LE}\rangle \langle \text{CS}| \right] + \sum_{\mu} g^{\mu}_{\text{CS, CS}} |\text{CS}\rangle \langle \text{CS}| (b_{\mu} + b_{\mu}^\dagger) \\
& + g^{R}_{\text{CS, CS}} |\text{CS}\rangle \langle \text{CS}| (b_{R} + b_{R}^\dagger) + g^{R}_{\text{LE, CS}} \left[|\text{CS}\rangle \langle \text{LE}| + |\text{LE}\rangle \langle \text{CS}|\right] (b_{R} + b_{R}^\dagger)\\
& + \omega_R b_R^\dagger b_R + \sum_{\mu} \omega_{\mu} b_{\mu}^\dagger b_{\mu}
\end{align}\end{split}\]
[3]:
backend = "numpy"
use_bath = True
epsilon = sympy.Symbol("ε")
t = sympy.Symbol("t_{LE, CS}")
g_cs = sympy.Symbol("g_{CS, CS}")
g_le = sympy.Symbol("g_{LE, CS}")
omega = sympy.Symbol("ω_R")
subs = {}
subs[epsilon] = -0.079 / units.au_in_eV
subs[t] = 0.130 / units.au_in_eV
subs[g_cs] = 0.001 * 30 / (2**0.5) / units.au_in_eV
subs[g_le] = -0.001 * 10 / (2**0.5) / units.au_in_eV
subs[omega] = 0.001 * 10 / units.au_in_eV
if use_bath:
bath_ω = (
np.array(
[
3.643,
7.286,
10.929,
14.573,
18.216,
21.859,
25.502,
29.145,
32.788,
36.431,
40.075,
43.718,
47.361,
51.004,
54.647,
58.29,
61.933,
65.577,
69.22,
72.863,
76.506,
80.149,
83.792,
87.435,
91.079,
94.722,
98.365,
102.008,
105.651,
109.294,
112.937,
116.581,
120.224,
123.867,
127.51,
131.153,
134.706,
138.439,
142.083,
145.726,
149.369,
153.012,
156.655,
160.298,
163.941,
167.585,
171.228,
174.871,
178.514,
182.157,
185.800,
189.443,
193.087,
196.730,
200.373,
204.016,
207.659,
211.302,
214.945,
218.589,
222.232,
225.875,
229.518,
233.161,
236.804,
240.447,
244.091,
247.734,
251.377,
255.020,
258.663,
262.306,
265.949,
269.593,
273.236,
276.879,
280.522,
284.165,
287.808,
291.451,
295.095,
298.738,
302.381,
306.024,
309.667,
313.310,
316.953,
320.597,
324.240,
327.883,
331.526,
335.169,
338.812,
342.455,
346.099,
349.742,
353.385,
357.028,
360.671,
]
)
/ 1000
/ units.au_in_eV
)
g_cs2 = (
np.array(
[
2.511,
2.359,
2.347,
2.586,
3.190,
4.203,
5.224,
5.741,
5.572,
5.547,
6.578,
8.456,
9.935,
10.056,
9.147,
8.002,
7.379,
8.038,
10.582,
14.242,
17.279,
18.380,
17.698,
15.808,
13.623,
12.158,
11.779,
12.196,
13.061,
13.549,
12.606,
10.303,
8.069,
7.192,
7.630,
8.721,
9.858,
10.601,
10.599,
10.123,
10.344,
12.335,
15.285,
16.939,
16.095,
14.735,
15.279,
19.071,
26.827,
38.225,
47.272,
47.873,
43.415,
39.088,
34.622,
28.686,
22.148,
16.585,
12.443,
9.701,
8.142,
7.254,
6.554,
5.910,
5.362,
4.932,
4.586,
4.287,
4.020,
3.785,
3.578,
3.395,
3.230,
3.081,
2.945,
2.822,
2.709,
2.605,
2.509,
2.420,
2.338,
2.262,
2.190,
2.123,
2.061,
2.003,
1.948,
1.897,
1.848,
1.803,
1.761,
1.721,
1.685,
1.650,
1.619,
1.593,
1.573,
1.552,
1.530,
]
)
/ 1000
/ units.au_in_eV
)
ω_symbols = [None]
g_symbols = [None]
for i, (ω, g) in enumerate(zip(bath_ω, g_cs2, strict=True)):
ω_symbols.append(sympy.Symbol(f"omega_{i + 2}"))
g_symbols.append(sympy.Symbol(f"g_{i + 2}"))
subs[ω_symbols[-1]] = ω
subs[g_symbols[-1]] = g
Setup basis for wavefunction
[4]:
basis = [
Exciton(nstate=2, names=["LE", "CS"]),
] + [Boson(nstate=28)] * len(ω_symbols)
basinfo = BasInfo([basis])
ndim = len(basis)
print(ndim)
101
Note
If you want more precise result, it may work to increase nstate of Boson.
Setup one particle operator
[5]:
a = basis[0].get_annihilation_matrix()
adag = basis[0].get_creation_matrix()
b = basis[1].get_annihilation_matrix()
bdag = basis[1].get_creation_matrix()
a_op = OpSite("a_0", 0, value=a)
adag_op = OpSite(r"a^\dagger_0", 0, value=adag)
b_ops = [None] + [
OpSite("b_{" + f"{i}" + "}", i, value=b) for i in range(1, ndim)
]
bdag_ops = [None] + [
OpSite(r"b^\dagger" + "_{" + f"{i}" + "}", i, value=bdag)
for i in range(1, ndim)
]
Setup potential and kinetic operator
[6]:
pot_sop = SumOfProducts()
pot_sop += adag_op * a_op * epsilon
pot_sop += (a_op + adag_op) * t
pot_sop += g_cs * adag_op * a_op * (b_ops[1] + bdag_ops[1])
pot_sop += g_le * a_op * (b_ops[1] + bdag_ops[1])
pot_sop += g_le * adag_op * (b_ops[1] + bdag_ops[1])
pot_sop += bdag_ops[1] * b_ops[1] * omega
for i in range(2, ndim):
pot_sop += g_symbols[i - 1] * adag_op * a_op * (b_ops[i] + bdag_ops[i])
for i in range(2, ndim):
pot_sop += ω_symbols[i - 1] * bdag_ops[i] * b_ops[i]
pot_sop = pot_sop.simplify()
pot_sop.symbol
[6]:
$\displaystyle g_{10} a^{\dagger}_{0} a_{0} \left(b^\dagger_{10} + b_{10}\right) + g_{100} a^{\dagger}_{0} a_{0} \left(b^\dagger_{100} + b_{100}\right) + g_{11} a^{\dagger}_{0} a_{0} \left(b^\dagger_{11} + b_{11}\right) + g_{12} a^{\dagger}_{0} a_{0} \left(b^\dagger_{12} + b_{12}\right) + g_{13} a^{\dagger}_{0} a_{0} \left(b^\dagger_{13} + b_{13}\right) + g_{14} a^{\dagger}_{0} a_{0} \left(b^\dagger_{14} + b_{14}\right) + g_{15} a^{\dagger}_{0} a_{0} \left(b^\dagger_{15} + b_{15}\right) + g_{16} a^{\dagger}_{0} a_{0} \left(b^\dagger_{16} + b_{16}\right) + g_{17} a^{\dagger}_{0} a_{0} \left(b^\dagger_{17} + b_{17}\right) + g_{18} a^{\dagger}_{0} a_{0} \left(b^\dagger_{18} + b_{18}\right) + g_{19} a^{\dagger}_{0} a_{0} \left(b^\dagger_{19} + b_{19}\right) + g_{2} a^{\dagger}_{0} a_{0} \left(b^\dagger_{2} + b_{2}\right) + g_{20} a^{\dagger}_{0} a_{0} \left(b^\dagger_{20} + b_{20}\right) + g_{21} a^{\dagger}_{0} a_{0} \left(b^\dagger_{21} + b_{21}\right) + g_{22} a^{\dagger}_{0} a_{0} \left(b^\dagger_{22} + b_{22}\right) + g_{23} a^{\dagger}_{0} a_{0} \left(b^\dagger_{23} + b_{23}\right) + g_{24} a^{\dagger}_{0} a_{0} \left(b^\dagger_{24} + b_{24}\right) + g_{25} a^{\dagger}_{0} a_{0} \left(b^\dagger_{25} + b_{25}\right) + g_{26} a^{\dagger}_{0} a_{0} \left(b^\dagger_{26} + b_{26}\right) + g_{27} a^{\dagger}_{0} a_{0} \left(b^\dagger_{27} + b_{27}\right) + g_{28} a^{\dagger}_{0} a_{0} \left(b^\dagger_{28} + b_{28}\right) + g_{29} a^{\dagger}_{0} a_{0} \left(b^\dagger_{29} + b_{29}\right) + g_{3} a^{\dagger}_{0} a_{0} \left(b^\dagger_{3} + b_{3}\right) + g_{30} a^{\dagger}_{0} a_{0} \left(b^\dagger_{30} + b_{30}\right) + g_{31} a^{\dagger}_{0} a_{0} \left(b^\dagger_{31} + b_{31}\right) + g_{32} a^{\dagger}_{0} a_{0} \left(b^\dagger_{32} + b_{32}\right) + g_{33} a^{\dagger}_{0} a_{0} \left(b^\dagger_{33} + b_{33}\right) + g_{34} a^{\dagger}_{0} a_{0} \left(b^\dagger_{34} + b_{34}\right) + g_{35} a^{\dagger}_{0} a_{0} \left(b^\dagger_{35} + b_{35}\right) + g_{36} a^{\dagger}_{0} a_{0} \left(b^\dagger_{36} + b_{36}\right) + g_{37} a^{\dagger}_{0} a_{0} \left(b^\dagger_{37} + b_{37}\right) + g_{38} a^{\dagger}_{0} a_{0} \left(b^\dagger_{38} + b_{38}\right) + g_{39} a^{\dagger}_{0} a_{0} \left(b^\dagger_{39} + b_{39}\right) + g_{4} a^{\dagger}_{0} a_{0} \left(b^\dagger_{4} + b_{4}\right) + g_{40} a^{\dagger}_{0} a_{0} \left(b^\dagger_{40} + b_{40}\right) + g_{41} a^{\dagger}_{0} a_{0} \left(b^\dagger_{41} + b_{41}\right) + g_{42} a^{\dagger}_{0} a_{0} \left(b^\dagger_{42} + b_{42}\right) + g_{43} a^{\dagger}_{0} a_{0} \left(b^\dagger_{43} + b_{43}\right) + g_{44} a^{\dagger}_{0} a_{0} \left(b^\dagger_{44} + b_{44}\right) + g_{45} a^{\dagger}_{0} a_{0} \left(b^\dagger_{45} + b_{45}\right) + g_{46} a^{\dagger}_{0} a_{0} \left(b^\dagger_{46} + b_{46}\right) + g_{47} a^{\dagger}_{0} a_{0} \left(b^\dagger_{47} + b_{47}\right) + g_{48} a^{\dagger}_{0} a_{0} \left(b^\dagger_{48} + b_{48}\right) + g_{49} a^{\dagger}_{0} a_{0} \left(b^\dagger_{49} + b_{49}\right) + g_{5} a^{\dagger}_{0} a_{0} \left(b^\dagger_{5} + b_{5}\right) + g_{50} a^{\dagger}_{0} a_{0} \left(b^\dagger_{50} + b_{50}\right) + g_{51} a^{\dagger}_{0} a_{0} \left(b^\dagger_{51} + b_{51}\right) + g_{52} a^{\dagger}_{0} a_{0} \left(b^\dagger_{52} + b_{52}\right) + g_{53} a^{\dagger}_{0} a_{0} \left(b^\dagger_{53} + b_{53}\right) + g_{54} a^{\dagger}_{0} a_{0} \left(b^\dagger_{54} + b_{54}\right) + g_{55} a^{\dagger}_{0} a_{0} \left(b^\dagger_{55} + b_{55}\right) + g_{56} a^{\dagger}_{0} a_{0} \left(b^\dagger_{56} + b_{56}\right) + g_{57} a^{\dagger}_{0} a_{0} \left(b^\dagger_{57} + b_{57}\right) + g_{58} a^{\dagger}_{0} a_{0} \left(b^\dagger_{58} + b_{58}\right) + g_{59} a^{\dagger}_{0} a_{0} \left(b^\dagger_{59} + b_{59}\right) + g_{6} a^{\dagger}_{0} a_{0} \left(b^\dagger_{6} + b_{6}\right) + g_{60} a^{\dagger}_{0} a_{0} \left(b^\dagger_{60} + b_{60}\right) + g_{61} a^{\dagger}_{0} a_{0} \left(b^\dagger_{61} + b_{61}\right) + g_{62} a^{\dagger}_{0} a_{0} \left(b^\dagger_{62} + b_{62}\right) + g_{63} a^{\dagger}_{0} a_{0} \left(b^\dagger_{63} + b_{63}\right) + g_{64} a^{\dagger}_{0} a_{0} \left(b^\dagger_{64} + b_{64}\right) + g_{65} a^{\dagger}_{0} a_{0} \left(b^\dagger_{65} + b_{65}\right) + g_{66} a^{\dagger}_{0} a_{0} \left(b^\dagger_{66} + b_{66}\right) + g_{67} a^{\dagger}_{0} a_{0} \left(b^\dagger_{67} + b_{67}\right) + g_{68} a^{\dagger}_{0} a_{0} \left(b^\dagger_{68} + b_{68}\right) + g_{69} a^{\dagger}_{0} a_{0} \left(b^\dagger_{69} + b_{69}\right) + g_{7} a^{\dagger}_{0} a_{0} \left(b^\dagger_{7} + b_{7}\right) + g_{70} a^{\dagger}_{0} a_{0} \left(b^\dagger_{70} + b_{70}\right) + g_{71} a^{\dagger}_{0} a_{0} \left(b^\dagger_{71} + b_{71}\right) + g_{72} a^{\dagger}_{0} a_{0} \left(b^\dagger_{72} + b_{72}\right) + g_{73} a^{\dagger}_{0} a_{0} \left(b^\dagger_{73} + b_{73}\right) + g_{74} a^{\dagger}_{0} a_{0} \left(b^\dagger_{74} + b_{74}\right) + g_{75} a^{\dagger}_{0} a_{0} \left(b^\dagger_{75} + b_{75}\right) + g_{76} a^{\dagger}_{0} a_{0} \left(b^\dagger_{76} + b_{76}\right) + g_{77} a^{\dagger}_{0} a_{0} \left(b^\dagger_{77} + b_{77}\right) + g_{78} a^{\dagger}_{0} a_{0} \left(b^\dagger_{78} + b_{78}\right) + g_{79} a^{\dagger}_{0} a_{0} \left(b^\dagger_{79} + b_{79}\right) + g_{8} a^{\dagger}_{0} a_{0} \left(b^\dagger_{8} + b_{8}\right) + g_{80} a^{\dagger}_{0} a_{0} \left(b^\dagger_{80} + b_{80}\right) + g_{81} a^{\dagger}_{0} a_{0} \left(b^\dagger_{81} + b_{81}\right) + g_{82} a^{\dagger}_{0} a_{0} \left(b^\dagger_{82} + b_{82}\right) + g_{83} a^{\dagger}_{0} a_{0} \left(b^\dagger_{83} + b_{83}\right) + g_{84} a^{\dagger}_{0} a_{0} \left(b^\dagger_{84} + b_{84}\right) + g_{85} a^{\dagger}_{0} a_{0} \left(b^\dagger_{85} + b_{85}\right) + g_{86} a^{\dagger}_{0} a_{0} \left(b^\dagger_{86} + b_{86}\right) + g_{87} a^{\dagger}_{0} a_{0} \left(b^\dagger_{87} + b_{87}\right) + g_{88} a^{\dagger}_{0} a_{0} \left(b^\dagger_{88} + b_{88}\right) + g_{89} a^{\dagger}_{0} a_{0} \left(b^\dagger_{89} + b_{89}\right) + g_{9} a^{\dagger}_{0} a_{0} \left(b^\dagger_{9} + b_{9}\right) + g_{90} a^{\dagger}_{0} a_{0} \left(b^\dagger_{90} + b_{90}\right) + g_{91} a^{\dagger}_{0} a_{0} \left(b^\dagger_{91} + b_{91}\right) + g_{92} a^{\dagger}_{0} a_{0} \left(b^\dagger_{92} + b_{92}\right) + g_{93} a^{\dagger}_{0} a_{0} \left(b^\dagger_{93} + b_{93}\right) + g_{94} a^{\dagger}_{0} a_{0} \left(b^\dagger_{94} + b_{94}\right) + g_{95} a^{\dagger}_{0} a_{0} \left(b^\dagger_{95} + b_{95}\right) + g_{96} a^{\dagger}_{0} a_{0} \left(b^\dagger_{96} + b_{96}\right) + g_{97} a^{\dagger}_{0} a_{0} \left(b^\dagger_{97} + b_{97}\right) + g_{98} a^{\dagger}_{0} a_{0} \left(b^\dagger_{98} + b_{98}\right) + g_{99} a^{\dagger}_{0} a_{0} \left(b^\dagger_{99} + b_{99}\right) + g_{CS, CS} a^{\dagger}_{0} a_{0} \left(b^\dagger_{1} + b_{1}\right) + g_{LE, CS} a^{\dagger}_{0} \left(b^\dagger_{1} + b_{1}\right) + g_{LE, CS} a_{0} \left(b^\dagger_{1} + b_{1}\right) + \omega_{10} b^\dagger_{10} b_{10} + \omega_{100} b^\dagger_{100} b_{100} + \omega_{11} b^\dagger_{11} b_{11} + \omega_{12} b^\dagger_{12} b_{12} + \omega_{13} b^\dagger_{13} b_{13} + \omega_{14} b^\dagger_{14} b_{14} + \omega_{15} b^\dagger_{15} b_{15} + \omega_{16} b^\dagger_{16} b_{16} + \omega_{17} b^\dagger_{17} b_{17} + \omega_{18} b^\dagger_{18} b_{18} + \omega_{19} b^\dagger_{19} b_{19} + \omega_{2} b^\dagger_{2} b_{2} + \omega_{20} b^\dagger_{20} b_{20} + \omega_{21} b^\dagger_{21} b_{21} + \omega_{22} b^\dagger_{22} b_{22} + \omega_{23} b^\dagger_{23} b_{23} + \omega_{24} b^\dagger_{24} b_{24} + \omega_{25} b^\dagger_{25} b_{25} + \omega_{26} b^\dagger_{26} b_{26} + \omega_{27} b^\dagger_{27} b_{27} + \omega_{28} b^\dagger_{28} b_{28} + \omega_{29} b^\dagger_{29} b_{29} + \omega_{3} b^\dagger_{3} b_{3} + \omega_{30} b^\dagger_{30} b_{30} + \omega_{31} b^\dagger_{31} b_{31} + \omega_{32} b^\dagger_{32} b_{32} + \omega_{33} b^\dagger_{33} b_{33} + \omega_{34} b^\dagger_{34} b_{34} + \omega_{35} b^\dagger_{35} b_{35} + \omega_{36} b^\dagger_{36} b_{36} + \omega_{37} b^\dagger_{37} b_{37} + \omega_{38} b^\dagger_{38} b_{38} + \omega_{39} b^\dagger_{39} b_{39} + \omega_{4} b^\dagger_{4} b_{4} + \omega_{40} b^\dagger_{40} b_{40} + \omega_{41} b^\dagger_{41} b_{41} + \omega_{42} b^\dagger_{42} b_{42} + \omega_{43} b^\dagger_{43} b_{43} + \omega_{44} b^\dagger_{44} b_{44} + \omega_{45} b^\dagger_{45} b_{45} + \omega_{46} b^\dagger_{46} b_{46} + \omega_{47} b^\dagger_{47} b_{47} + \omega_{48} b^\dagger_{48} b_{48} + \omega_{49} b^\dagger_{49} b_{49} + \omega_{5} b^\dagger_{5} b_{5} + \omega_{50} b^\dagger_{50} b_{50} + \omega_{51} b^\dagger_{51} b_{51} + \omega_{52} b^\dagger_{52} b_{52} + \omega_{53} b^\dagger_{53} b_{53} + \omega_{54} b^\dagger_{54} b_{54} + \omega_{55} b^\dagger_{55} b_{55} + \omega_{56} b^\dagger_{56} b_{56} + \omega_{57} b^\dagger_{57} b_{57} + \omega_{58} b^\dagger_{58} b_{58} + \omega_{59} b^\dagger_{59} b_{59} + \omega_{6} b^\dagger_{6} b_{6} + \omega_{60} b^\dagger_{60} b_{60} + \omega_{61} b^\dagger_{61} b_{61} + \omega_{62} b^\dagger_{62} b_{62} + \omega_{63} b^\dagger_{63} b_{63} + \omega_{64} b^\dagger_{64} b_{64} + \omega_{65} b^\dagger_{65} b_{65} + \omega_{66} b^\dagger_{66} b_{66} + \omega_{67} b^\dagger_{67} b_{67} + \omega_{68} b^\dagger_{68} b_{68} + \omega_{69} b^\dagger_{69} b_{69} + \omega_{7} b^\dagger_{7} b_{7} + \omega_{70} b^\dagger_{70} b_{70} + \omega_{71} b^\dagger_{71} b_{71} + \omega_{72} b^\dagger_{72} b_{72} + \omega_{73} b^\dagger_{73} b_{73} + \omega_{74} b^\dagger_{74} b_{74} + \omega_{75} b^\dagger_{75} b_{75} + \omega_{76} b^\dagger_{76} b_{76} + \omega_{77} b^\dagger_{77} b_{77} + \omega_{78} b^\dagger_{78} b_{78} + \omega_{79} b^\dagger_{79} b_{79} + \omega_{8} b^\dagger_{8} b_{8} + \omega_{80} b^\dagger_{80} b_{80} + \omega_{81} b^\dagger_{81} b_{81} + \omega_{82} b^\dagger_{82} b_{82} + \omega_{83} b^\dagger_{83} b_{83} + \omega_{84} b^\dagger_{84} b_{84} + \omega_{85} b^\dagger_{85} b_{85} + \omega_{86} b^\dagger_{86} b_{86} + \omega_{87} b^\dagger_{87} b_{87} + \omega_{88} b^\dagger_{88} b_{88} + \omega_{89} b^\dagger_{89} b_{89} + \omega_{9} b^\dagger_{9} b_{9} + \omega_{90} b^\dagger_{90} b_{90} + \omega_{91} b^\dagger_{91} b_{91} + \omega_{92} b^\dagger_{92} b_{92} + \omega_{93} b^\dagger_{93} b_{93} + \omega_{94} b^\dagger_{94} b_{94} + \omega_{95} b^\dagger_{95} b_{95} + \omega_{96} b^\dagger_{96} b_{96} + \omega_{97} b^\dagger_{97} b_{97} + \omega_{98} b^\dagger_{98} b_{98} + \omega_{99} b^\dagger_{99} b_{99} + t_{LE, CS} \left(a^{\dagger}_{0} + a_{0}\right) + ε a^{\dagger}_{0} a_{0} + ω_{R} b^\dagger_{1} b_{1}$
Setup MPO
[7]:
am_pot = AssignManager(pot_sop)
am_pot.assign()
display(*am_pot.Wsym)
W_prod = sympy.Mul(*am_pot.Wsym)
print(*[f"W{i}" for i in range(am_pot.ndim)], "=")
display(W_prod[0].expand())
pot_mpo = am_pot.numerical_mpo(subs=subs)
$\displaystyle \left[\begin{matrix}a^{\dagger}_{0} + a_{0} & a^{\dagger}_{0} a_{0} & 1 & g_{LE, CS} a^{\dagger}_{0} + g_{LE, CS} a_{0}\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 0 & t_{LE, CS}\\0 & 1 & g_{CS, CS} \left(b^\dagger_{1} + b_{1}\right)\\1 & 0 & ω_{R} b^\dagger_{1} b_{1}\\0 & 0 & b^\dagger_{1} + b_{1}\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{2} b^\dagger_{2} b_{2}\\1 & 0 & g_{2} \left(b^\dagger_{2} + b_{2}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{3} \left(b^\dagger_{3} + b_{3}\right)\\0 & 1 & \omega_{3} b^\dagger_{3} b_{3}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{4} \left(b^\dagger_{4} + b_{4}\right)\\0 & 1 & \omega_{4} b^\dagger_{4} b_{4}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{5} \left(b^\dagger_{5} + b_{5}\right)\\0 & 1 & \omega_{5} b^\dagger_{5} b_{5}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{6} \left(b^\dagger_{6} + b_{6}\right)\\1 & 0 & \omega_{6} b^\dagger_{6} b_{6}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{7} b^\dagger_{7} b_{7}\\0 & 1 & g_{7} \left(b^\dagger_{7} + b_{7}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{8} b^\dagger_{8} b_{8}\\0 & 1 & g_{8} \left(b^\dagger_{8} + b_{8}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{9} b^\dagger_{9} b_{9}\\1 & 0 & g_{9} \left(b^\dagger_{9} + b_{9}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{10} \left(b^\dagger_{10} + b_{10}\right)\\1 & 0 & \omega_{10} b^\dagger_{10} b_{10}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{11} b^\dagger_{11} b_{11}\\0 & 1 & g_{11} \left(b^\dagger_{11} + b_{11}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{12} b^\dagger_{12} b_{12}\\1 & 0 & g_{12} \left(b^\dagger_{12} + b_{12}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{13} \left(b^\dagger_{13} + b_{13}\right)\\0 & 1 & \omega_{13} b^\dagger_{13} b_{13}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{14} \left(b^\dagger_{14} + b_{14}\right)\\1 & 0 & \omega_{14} b^\dagger_{14} b_{14}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{15} b^\dagger_{15} b_{15}\\0 & 1 & g_{15} \left(b^\dagger_{15} + b_{15}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{16} b^\dagger_{16} b_{16}\\1 & 0 & g_{16} \left(b^\dagger_{16} + b_{16}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{17} \left(b^\dagger_{17} + b_{17}\right)\\1 & 0 & \omega_{17} b^\dagger_{17} b_{17}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{18} b^\dagger_{18} b_{18}\\0 & 1 & g_{18} \left(b^\dagger_{18} + b_{18}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{19} b^\dagger_{19} b_{19}\\1 & 0 & g_{19} \left(b^\dagger_{19} + b_{19}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{20} \left(b^\dagger_{20} + b_{20}\right)\\0 & 1 & \omega_{20} b^\dagger_{20} b_{20}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{21} \left(b^\dagger_{21} + b_{21}\right)\\0 & 1 & \omega_{21} b^\dagger_{21} b_{21}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{22} \left(b^\dagger_{22} + b_{22}\right)\\0 & 1 & \omega_{22} b^\dagger_{22} b_{22}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{23} \left(b^\dagger_{23} + b_{23}\right)\\1 & 0 & \omega_{23} b^\dagger_{23} b_{23}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{24} b^\dagger_{24} b_{24}\\0 & 1 & g_{24} \left(b^\dagger_{24} + b_{24}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{25} b^\dagger_{25} b_{25}\\0 & 1 & g_{25} \left(b^\dagger_{25} + b_{25}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{26} b^\dagger_{26} b_{26}\\0 & 1 & g_{26} \left(b^\dagger_{26} + b_{26}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{27} b^\dagger_{27} b_{27}\\0 & 1 & g_{27} \left(b^\dagger_{27} + b_{27}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{28} b^\dagger_{28} b_{28}\\1 & 0 & g_{28} \left(b^\dagger_{28} + b_{28}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{29} \left(b^\dagger_{29} + b_{29}\right)\\0 & 1 & \omega_{29} b^\dagger_{29} b_{29}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{30} \left(b^\dagger_{30} + b_{30}\right)\\0 & 1 & \omega_{30} b^\dagger_{30} b_{30}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{31} \left(b^\dagger_{31} + b_{31}\right)\\1 & 0 & \omega_{31} b^\dagger_{31} b_{31}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{32} b^\dagger_{32} b_{32}\\0 & 1 & g_{32} \left(b^\dagger_{32} + b_{32}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{33} b^\dagger_{33} b_{33}\\1 & 0 & g_{33} \left(b^\dagger_{33} + b_{33}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{34} \left(b^\dagger_{34} + b_{34}\right)\\0 & 1 & \omega_{34} b^\dagger_{34} b_{34}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{35} \left(b^\dagger_{35} + b_{35}\right)\\1 & 0 & \omega_{35} b^\dagger_{35} b_{35}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{36} b^\dagger_{36} b_{36}\\1 & 0 & g_{36} \left(b^\dagger_{36} + b_{36}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{37} \left(b^\dagger_{37} + b_{37}\right)\\1 & 0 & \omega_{37} b^\dagger_{37} b_{37}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{38} b^\dagger_{38} b_{38}\\0 & 1 & g_{38} \left(b^\dagger_{38} + b_{38}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{39} b^\dagger_{39} b_{39}\\1 & 0 & g_{39} \left(b^\dagger_{39} + b_{39}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{40} \left(b^\dagger_{40} + b_{40}\right)\\0 & 1 & \omega_{40} b^\dagger_{40} b_{40}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{41} \left(b^\dagger_{41} + b_{41}\right)\\1 & 0 & \omega_{41} b^\dagger_{41} b_{41}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{42} b^\dagger_{42} b_{42}\\0 & 1 & g_{42} \left(b^\dagger_{42} + b_{42}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{43} b^\dagger_{43} b_{43}\\0 & 1 & g_{43} \left(b^\dagger_{43} + b_{43}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{44} b^\dagger_{44} b_{44}\\0 & 1 & g_{44} \left(b^\dagger_{44} + b_{44}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{45} b^\dagger_{45} b_{45}\\1 & 0 & g_{45} \left(b^\dagger_{45} + b_{45}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{46} \left(b^\dagger_{46} + b_{46}\right)\\0 & 1 & \omega_{46} b^\dagger_{46} b_{46}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{47} \left(b^\dagger_{47} + b_{47}\right)\\1 & 0 & \omega_{47} b^\dagger_{47} b_{47}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{48} b^\dagger_{48} b_{48}\\1 & 0 & g_{48} \left(b^\dagger_{48} + b_{48}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{49} \left(b^\dagger_{49} + b_{49}\right)\\0 & 1 & \omega_{49} b^\dagger_{49} b_{49}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{50} \left(b^\dagger_{50} + b_{50}\right)\\0 & 1 & \omega_{50} b^\dagger_{50} b_{50}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{51} \left(b^\dagger_{51} + b_{51}\right)\\0 & 1 & \omega_{51} b^\dagger_{51} b_{51}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{52} \left(b^\dagger_{52} + b_{52}\right)\\0 & 1 & \omega_{52} b^\dagger_{52} b_{52}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{53} \left(b^\dagger_{53} + b_{53}\right)\\0 & 1 & \omega_{53} b^\dagger_{53} b_{53}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{54} \left(b^\dagger_{54} + b_{54}\right)\\0 & 1 & \omega_{54} b^\dagger_{54} b_{54}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{55} \left(b^\dagger_{55} + b_{55}\right)\\0 & 1 & \omega_{55} b^\dagger_{55} b_{55}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{56} \left(b^\dagger_{56} + b_{56}\right)\\0 & 1 & \omega_{56} b^\dagger_{56} b_{56}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{57} \left(b^\dagger_{57} + b_{57}\right)\\1 & 0 & \omega_{57} b^\dagger_{57} b_{57}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{58} b^\dagger_{58} b_{58}\\0 & 1 & g_{58} \left(b^\dagger_{58} + b_{58}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{59} b^\dagger_{59} b_{59}\\0 & 1 & g_{59} \left(b^\dagger_{59} + b_{59}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{60} b^\dagger_{60} b_{60}\\1 & 0 & g_{60} \left(b^\dagger_{60} + b_{60}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{61} \left(b^\dagger_{61} + b_{61}\right)\\1 & 0 & \omega_{61} b^\dagger_{61} b_{61}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{62} b^\dagger_{62} b_{62}\\0 & 1 & g_{62} \left(b^\dagger_{62} + b_{62}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{63} b^\dagger_{63} b_{63}\\1 & 0 & g_{63} \left(b^\dagger_{63} + b_{63}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{64} \left(b^\dagger_{64} + b_{64}\right)\\1 & 0 & \omega_{64} b^\dagger_{64} b_{64}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{65} b^\dagger_{65} b_{65}\\0 & 1 & g_{65} \left(b^\dagger_{65} + b_{65}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{66} b^\dagger_{66} b_{66}\\1 & 0 & g_{66} \left(b^\dagger_{66} + b_{66}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{67} \left(b^\dagger_{67} + b_{67}\right)\\1 & 0 & \omega_{67} b^\dagger_{67} b_{67}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{68} b^\dagger_{68} b_{68}\\1 & 0 & g_{68} \left(b^\dagger_{68} + b_{68}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{69} \left(b^\dagger_{69} + b_{69}\right)\\1 & 0 & \omega_{69} b^\dagger_{69} b_{69}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{70} b^\dagger_{70} b_{70}\\1 & 0 & g_{70} \left(b^\dagger_{70} + b_{70}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{71} \left(b^\dagger_{71} + b_{71}\right)\\1 & 0 & \omega_{71} b^\dagger_{71} b_{71}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{72} b^\dagger_{72} b_{72}\\1 & 0 & g_{72} \left(b^\dagger_{72} + b_{72}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{73} \left(b^\dagger_{73} + b_{73}\right)\\0 & 1 & \omega_{73} b^\dagger_{73} b_{73}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{74} \left(b^\dagger_{74} + b_{74}\right)\\1 & 0 & \omega_{74} b^\dagger_{74} b_{74}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{75} b^\dagger_{75} b_{75}\\0 & 1 & g_{75} \left(b^\dagger_{75} + b_{75}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{76} b^\dagger_{76} b_{76}\\0 & 1 & g_{76} \left(b^\dagger_{76} + b_{76}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{77} b^\dagger_{77} b_{77}\\0 & 1 & g_{77} \left(b^\dagger_{77} + b_{77}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{78} b^\dagger_{78} b_{78}\\0 & 1 & g_{78} \left(b^\dagger_{78} + b_{78}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{79} b^\dagger_{79} b_{79}\\1 & 0 & g_{79} \left(b^\dagger_{79} + b_{79}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{80} \left(b^\dagger_{80} + b_{80}\right)\\0 & 1 & \omega_{80} b^\dagger_{80} b_{80}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{81} \left(b^\dagger_{81} + b_{81}\right)\\1 & 0 & \omega_{81} b^\dagger_{81} b_{81}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{82} b^\dagger_{82} b_{82}\\1 & 0 & g_{82} \left(b^\dagger_{82} + b_{82}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{83} \left(b^\dagger_{83} + b_{83}\right)\\1 & 0 & \omega_{83} b^\dagger_{83} b_{83}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{84} b^\dagger_{84} b_{84}\\0 & 1 & g_{84} \left(b^\dagger_{84} + b_{84}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & \omega_{85} b^\dagger_{85} b_{85}\\0 & 1 & g_{85} \left(b^\dagger_{85} + b_{85}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{86} b^\dagger_{86} b_{86}\\1 & 0 & g_{86} \left(b^\dagger_{86} + b_{86}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{87} \left(b^\dagger_{87} + b_{87}\right)\\1 & 0 & \omega_{87} b^\dagger_{87} b_{87}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{88} b^\dagger_{88} b_{88}\\1 & 0 & g_{88} \left(b^\dagger_{88} + b_{88}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{89} \left(b^\dagger_{89} + b_{89}\right)\\0 & 1 & \omega_{89} b^\dagger_{89} b_{89}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{90} \left(b^\dagger_{90} + b_{90}\right)\\0 & 1 & \omega_{90} b^\dagger_{90} b_{90}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{91} \left(b^\dagger_{91} + b_{91}\right)\\0 & 1 & \omega_{91} b^\dagger_{91} b_{91}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{92} \left(b^\dagger_{92} + b_{92}\right)\\0 & 1 & \omega_{92} b^\dagger_{92} b_{92}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{93} \left(b^\dagger_{93} + b_{93}\right)\\1 & 0 & \omega_{93} b^\dagger_{93} b_{93}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{94} b^\dagger_{94} b_{94}\\1 & 0 & g_{94} \left(b^\dagger_{94} + b_{94}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{95} \left(b^\dagger_{95} + b_{95}\right)\\0 & 1 & \omega_{95} b^\dagger_{95} b_{95}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{96} \left(b^\dagger_{96} + b_{96}\right)\\1 & 0 & \omega_{96} b^\dagger_{96} b_{96}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & \omega_{97} b^\dagger_{97} b_{97}\\1 & 0 & g_{97} \left(b^\dagger_{97} + b_{97}\right)\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}1 & 0 & g_{98} \left(b^\dagger_{98} + b_{98}\right)\\0 & 1 & \omega_{98} b^\dagger_{98} b_{98}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}0 & 1 & g_{99} \left(b^\dagger_{99} + b_{99}\right)\\1 & 0 & \omega_{99} b^\dagger_{99} b_{99}\\0 & 0 & 1\end{matrix}\right]$
$\displaystyle \left[\begin{matrix}\omega_{100} b^\dagger_{100} b_{100}\\g_{100} \left(b^\dagger_{100} + b_{100}\right) + ε\\1\end{matrix}\right]$
W0 W1 W2 W3 W4 W5 W6 W7 W8 W9 W10 W11 W12 W13 W14 W15 W16 W17 W18 W19 W20 W21 W22 W23 W24 W25 W26 W27 W28 W29 W30 W31 W32 W33 W34 W35 W36 W37 W38 W39 W40 W41 W42 W43 W44 W45 W46 W47 W48 W49 W50 W51 W52 W53 W54 W55 W56 W57 W58 W59 W60 W61 W62 W63 W64 W65 W66 W67 W68 W69 W70 W71 W72 W73 W74 W75 W76 W77 W78 W79 W80 W81 W82 W83 W84 W85 W86 W87 W88 W89 W90 W91 W92 W93 W94 W95 W96 W97 W98 W99 W100 =
$\displaystyle g_{10} a^{\dagger}_{0} a_{0} b^\dagger_{10} + g_{10} a^{\dagger}_{0} a_{0} b_{10} + g_{100} a^{\dagger}_{0} a_{0} b^\dagger_{100} + g_{100} a^{\dagger}_{0} a_{0} b_{100} + g_{11} a^{\dagger}_{0} a_{0} b^\dagger_{11} + g_{11} a^{\dagger}_{0} a_{0} b_{11} + g_{12} a^{\dagger}_{0} a_{0} b^\dagger_{12} + g_{12} a^{\dagger}_{0} a_{0} b_{12} + g_{13} a^{\dagger}_{0} a_{0} b^\dagger_{13} + g_{13} a^{\dagger}_{0} a_{0} b_{13} + g_{14} a^{\dagger}_{0} a_{0} b^\dagger_{14} + g_{14} a^{\dagger}_{0} a_{0} b_{14} + g_{15} a^{\dagger}_{0} a_{0} b^\dagger_{15} + g_{15} a^{\dagger}_{0} a_{0} b_{15} + g_{16} a^{\dagger}_{0} a_{0} b^\dagger_{16} + g_{16} a^{\dagger}_{0} a_{0} b_{16} + g_{17} a^{\dagger}_{0} a_{0} b^\dagger_{17} + g_{17} a^{\dagger}_{0} a_{0} b_{17} + g_{18} a^{\dagger}_{0} a_{0} b^\dagger_{18} + g_{18} a^{\dagger}_{0} a_{0} b_{18} + g_{19} a^{\dagger}_{0} a_{0} b^\dagger_{19} + g_{19} a^{\dagger}_{0} a_{0} b_{19} + g_{2} a^{\dagger}_{0} a_{0} b^\dagger_{2} + g_{2} a^{\dagger}_{0} a_{0} b_{2} + g_{20} a^{\dagger}_{0} a_{0} b^\dagger_{20} + g_{20} a^{\dagger}_{0} a_{0} b_{20} + g_{21} a^{\dagger}_{0} a_{0} b^\dagger_{21} + g_{21} a^{\dagger}_{0} a_{0} b_{21} + g_{22} a^{\dagger}_{0} a_{0} b^\dagger_{22} + g_{22} a^{\dagger}_{0} a_{0} b_{22} + g_{23} a^{\dagger}_{0} a_{0} b^\dagger_{23} + g_{23} a^{\dagger}_{0} a_{0} b_{23} + g_{24} a^{\dagger}_{0} a_{0} b^\dagger_{24} + g_{24} a^{\dagger}_{0} a_{0} b_{24} + g_{25} a^{\dagger}_{0} a_{0} b^\dagger_{25} + g_{25} a^{\dagger}_{0} a_{0} b_{25} + g_{26} a^{\dagger}_{0} a_{0} b^\dagger_{26} + g_{26} a^{\dagger}_{0} a_{0} b_{26} + g_{27} a^{\dagger}_{0} a_{0} b^\dagger_{27} + g_{27} a^{\dagger}_{0} a_{0} b_{27} + g_{28} a^{\dagger}_{0} a_{0} b^\dagger_{28} + g_{28} a^{\dagger}_{0} a_{0} b_{28} + g_{29} a^{\dagger}_{0} a_{0} b^\dagger_{29} + g_{29} a^{\dagger}_{0} a_{0} b_{29} + g_{3} a^{\dagger}_{0} a_{0} b^\dagger_{3} + g_{3} a^{\dagger}_{0} a_{0} b_{3} + g_{30} a^{\dagger}_{0} a_{0} b^\dagger_{30} + g_{30} a^{\dagger}_{0} a_{0} b_{30} + g_{31} a^{\dagger}_{0} a_{0} b^\dagger_{31} + g_{31} a^{\dagger}_{0} a_{0} b_{31} + g_{32} a^{\dagger}_{0} a_{0} b^\dagger_{32} + g_{32} a^{\dagger}_{0} a_{0} b_{32} + g_{33} a^{\dagger}_{0} a_{0} b^\dagger_{33} + g_{33} a^{\dagger}_{0} a_{0} b_{33} + g_{34} a^{\dagger}_{0} a_{0} b^\dagger_{34} + g_{34} a^{\dagger}_{0} a_{0} b_{34} + g_{35} a^{\dagger}_{0} a_{0} b^\dagger_{35} + g_{35} a^{\dagger}_{0} a_{0} b_{35} + g_{36} a^{\dagger}_{0} a_{0} b^\dagger_{36} + g_{36} a^{\dagger}_{0} a_{0} b_{36} + g_{37} a^{\dagger}_{0} a_{0} b^\dagger_{37} + g_{37} a^{\dagger}_{0} a_{0} b_{37} + g_{38} a^{\dagger}_{0} a_{0} b^\dagger_{38} + g_{38} a^{\dagger}_{0} a_{0} b_{38} + g_{39} a^{\dagger}_{0} a_{0} b^\dagger_{39} + g_{39} a^{\dagger}_{0} a_{0} b_{39} + g_{4} a^{\dagger}_{0} a_{0} b^\dagger_{4} + g_{4} a^{\dagger}_{0} a_{0} b_{4} + g_{40} a^{\dagger}_{0} a_{0} b^\dagger_{40} + g_{40} a^{\dagger}_{0} a_{0} b_{40} + g_{41} a^{\dagger}_{0} a_{0} b^\dagger_{41} + g_{41} a^{\dagger}_{0} a_{0} b_{41} + g_{42} a^{\dagger}_{0} a_{0} b^\dagger_{42} + g_{42} a^{\dagger}_{0} a_{0} b_{42} + g_{43} a^{\dagger}_{0} a_{0} b^\dagger_{43} + g_{43} a^{\dagger}_{0} a_{0} b_{43} + g_{44} a^{\dagger}_{0} a_{0} b^\dagger_{44} + g_{44} a^{\dagger}_{0} a_{0} b_{44} + g_{45} a^{\dagger}_{0} a_{0} b^\dagger_{45} + g_{45} a^{\dagger}_{0} a_{0} b_{45} + g_{46} a^{\dagger}_{0} a_{0} b^\dagger_{46} + g_{46} a^{\dagger}_{0} a_{0} b_{46} + g_{47} a^{\dagger}_{0} a_{0} b^\dagger_{47} + g_{47} a^{\dagger}_{0} a_{0} b_{47} + g_{48} a^{\dagger}_{0} a_{0} b^\dagger_{48} + g_{48} a^{\dagger}_{0} a_{0} b_{48} + g_{49} a^{\dagger}_{0} a_{0} b^\dagger_{49} + g_{49} a^{\dagger}_{0} a_{0} b_{49} + g_{5} a^{\dagger}_{0} a_{0} b^\dagger_{5} + g_{5} a^{\dagger}_{0} a_{0} b_{5} + g_{50} a^{\dagger}_{0} a_{0} b^\dagger_{50} + g_{50} a^{\dagger}_{0} a_{0} b_{50} + g_{51} a^{\dagger}_{0} a_{0} b^\dagger_{51} + g_{51} a^{\dagger}_{0} a_{0} b_{51} + g_{52} a^{\dagger}_{0} a_{0} b^\dagger_{52} + g_{52} a^{\dagger}_{0} a_{0} b_{52} + g_{53} a^{\dagger}_{0} a_{0} b^\dagger_{53} + g_{53} a^{\dagger}_{0} a_{0} b_{53} + g_{54} a^{\dagger}_{0} a_{0} b^\dagger_{54} + g_{54} a^{\dagger}_{0} a_{0} b_{54} + g_{55} a^{\dagger}_{0} a_{0} b^\dagger_{55} + g_{55} a^{\dagger}_{0} a_{0} b_{55} + g_{56} a^{\dagger}_{0} a_{0} b^\dagger_{56} + g_{56} a^{\dagger}_{0} a_{0} b_{56} + g_{57} a^{\dagger}_{0} a_{0} b^\dagger_{57} + g_{57} a^{\dagger}_{0} a_{0} b_{57} + g_{58} a^{\dagger}_{0} a_{0} b^\dagger_{58} + g_{58} a^{\dagger}_{0} a_{0} b_{58} + g_{59} a^{\dagger}_{0} a_{0} b^\dagger_{59} + g_{59} a^{\dagger}_{0} a_{0} b_{59} + g_{6} a^{\dagger}_{0} a_{0} b^\dagger_{6} + g_{6} a^{\dagger}_{0} a_{0} b_{6} + g_{60} a^{\dagger}_{0} a_{0} b^\dagger_{60} + g_{60} a^{\dagger}_{0} a_{0} b_{60} + g_{61} a^{\dagger}_{0} a_{0} b^\dagger_{61} + g_{61} a^{\dagger}_{0} a_{0} b_{61} + g_{62} a^{\dagger}_{0} a_{0} b^\dagger_{62} + g_{62} a^{\dagger}_{0} a_{0} b_{62} + g_{63} a^{\dagger}_{0} a_{0} b^\dagger_{63} + g_{63} a^{\dagger}_{0} a_{0} b_{63} + g_{64} a^{\dagger}_{0} a_{0} b^\dagger_{64} + g_{64} a^{\dagger}_{0} a_{0} b_{64} + g_{65} a^{\dagger}_{0} a_{0} b^\dagger_{65} + g_{65} a^{\dagger}_{0} a_{0} b_{65} + g_{66} a^{\dagger}_{0} a_{0} b^\dagger_{66} + g_{66} a^{\dagger}_{0} a_{0} b_{66} + g_{67} a^{\dagger}_{0} a_{0} b^\dagger_{67} + g_{67} a^{\dagger}_{0} a_{0} b_{67} + g_{68} a^{\dagger}_{0} a_{0} b^\dagger_{68} + g_{68} a^{\dagger}_{0} a_{0} b_{68} + g_{69} a^{\dagger}_{0} a_{0} b^\dagger_{69} + g_{69} a^{\dagger}_{0} a_{0} b_{69} + g_{7} a^{\dagger}_{0} a_{0} b^\dagger_{7} + g_{7} a^{\dagger}_{0} a_{0} b_{7} + g_{70} a^{\dagger}_{0} a_{0} b^\dagger_{70} + g_{70} a^{\dagger}_{0} a_{0} b_{70} + g_{71} a^{\dagger}_{0} a_{0} b^\dagger_{71} + g_{71} a^{\dagger}_{0} a_{0} b_{71} + g_{72} a^{\dagger}_{0} a_{0} b^\dagger_{72} + g_{72} a^{\dagger}_{0} a_{0} b_{72} + g_{73} a^{\dagger}_{0} a_{0} b^\dagger_{73} + g_{73} a^{\dagger}_{0} a_{0} b_{73} + g_{74} a^{\dagger}_{0} a_{0} b^\dagger_{74} + g_{74} a^{\dagger}_{0} a_{0} b_{74} + g_{75} a^{\dagger}_{0} a_{0} b^\dagger_{75} + g_{75} a^{\dagger}_{0} a_{0} b_{75} + g_{76} a^{\dagger}_{0} a_{0} b^\dagger_{76} + g_{76} a^{\dagger}_{0} a_{0} b_{76} + g_{77} a^{\dagger}_{0} a_{0} b^\dagger_{77} + g_{77} a^{\dagger}_{0} a_{0} b_{77} + g_{78} a^{\dagger}_{0} a_{0} b^\dagger_{78} + g_{78} a^{\dagger}_{0} a_{0} b_{78} + g_{79} a^{\dagger}_{0} a_{0} b^\dagger_{79} + g_{79} a^{\dagger}_{0} a_{0} b_{79} + g_{8} a^{\dagger}_{0} a_{0} b^\dagger_{8} + g_{8} a^{\dagger}_{0} a_{0} b_{8} + g_{80} a^{\dagger}_{0} a_{0} b^\dagger_{80} + g_{80} a^{\dagger}_{0} a_{0} b_{80} + g_{81} a^{\dagger}_{0} a_{0} b^\dagger_{81} + g_{81} a^{\dagger}_{0} a_{0} b_{81} + g_{82} a^{\dagger}_{0} a_{0} b^\dagger_{82} + g_{82} a^{\dagger}_{0} a_{0} b_{82} + g_{83} a^{\dagger}_{0} a_{0} b^\dagger_{83} + g_{83} a^{\dagger}_{0} a_{0} b_{83} + g_{84} a^{\dagger}_{0} a_{0} b^\dagger_{84} + g_{84} a^{\dagger}_{0} a_{0} b_{84} + g_{85} a^{\dagger}_{0} a_{0} b^\dagger_{85} + g_{85} a^{\dagger}_{0} a_{0} b_{85} + g_{86} a^{\dagger}_{0} a_{0} b^\dagger_{86} + g_{86} a^{\dagger}_{0} a_{0} b_{86} + g_{87} a^{\dagger}_{0} a_{0} b^\dagger_{87} + g_{87} a^{\dagger}_{0} a_{0} b_{87} + g_{88} a^{\dagger}_{0} a_{0} b^\dagger_{88} + g_{88} a^{\dagger}_{0} a_{0} b_{88} + g_{89} a^{\dagger}_{0} a_{0} b^\dagger_{89} + g_{89} a^{\dagger}_{0} a_{0} b_{89} + g_{9} a^{\dagger}_{0} a_{0} b^\dagger_{9} + g_{9} a^{\dagger}_{0} a_{0} b_{9} + g_{90} a^{\dagger}_{0} a_{0} b^\dagger_{90} + g_{90} a^{\dagger}_{0} a_{0} b_{90} + g_{91} a^{\dagger}_{0} a_{0} b^\dagger_{91} + g_{91} a^{\dagger}_{0} a_{0} b_{91} + g_{92} a^{\dagger}_{0} a_{0} b^\dagger_{92} + g_{92} a^{\dagger}_{0} a_{0} b_{92} + g_{93} a^{\dagger}_{0} a_{0} b^\dagger_{93} + g_{93} a^{\dagger}_{0} a_{0} b_{93} + g_{94} a^{\dagger}_{0} a_{0} b^\dagger_{94} + g_{94} a^{\dagger}_{0} a_{0} b_{94} + g_{95} a^{\dagger}_{0} a_{0} b^\dagger_{95} + g_{95} a^{\dagger}_{0} a_{0} b_{95} + g_{96} a^{\dagger}_{0} a_{0} b^\dagger_{96} + g_{96} a^{\dagger}_{0} a_{0} b_{96} + g_{97} a^{\dagger}_{0} a_{0} b^\dagger_{97} + g_{97} a^{\dagger}_{0} a_{0} b_{97} + g_{98} a^{\dagger}_{0} a_{0} b^\dagger_{98} + g_{98} a^{\dagger}_{0} a_{0} b_{98} + g_{99} a^{\dagger}_{0} a_{0} b^\dagger_{99} + g_{99} a^{\dagger}_{0} a_{0} b_{99} + g_{CS, CS} a^{\dagger}_{0} a_{0} b^\dagger_{1} + g_{CS, CS} a^{\dagger}_{0} a_{0} b_{1} + g_{LE, CS} a^{\dagger}_{0} b^\dagger_{1} + g_{LE, CS} a^{\dagger}_{0} b_{1} + g_{LE, CS} a_{0} b^\dagger_{1} + g_{LE, CS} a_{0} b_{1} + \omega_{10} b^\dagger_{10} b_{10} + \omega_{100} b^\dagger_{100} b_{100} + \omega_{11} b^\dagger_{11} b_{11} + \omega_{12} b^\dagger_{12} b_{12} + \omega_{13} b^\dagger_{13} b_{13} + \omega_{14} b^\dagger_{14} b_{14} + \omega_{15} b^\dagger_{15} b_{15} + \omega_{16} b^\dagger_{16} b_{16} + \omega_{17} b^\dagger_{17} b_{17} + \omega_{18} b^\dagger_{18} b_{18} + \omega_{19} b^\dagger_{19} b_{19} + \omega_{2} b^\dagger_{2} b_{2} + \omega_{20} b^\dagger_{20} b_{20} + \omega_{21} b^\dagger_{21} b_{21} + \omega_{22} b^\dagger_{22} b_{22} + \omega_{23} b^\dagger_{23} b_{23} + \omega_{24} b^\dagger_{24} b_{24} + \omega_{25} b^\dagger_{25} b_{25} + \omega_{26} b^\dagger_{26} b_{26} + \omega_{27} b^\dagger_{27} b_{27} + \omega_{28} b^\dagger_{28} b_{28} + \omega_{29} b^\dagger_{29} b_{29} + \omega_{3} b^\dagger_{3} b_{3} + \omega_{30} b^\dagger_{30} b_{30} + \omega_{31} b^\dagger_{31} b_{31} + \omega_{32} b^\dagger_{32} b_{32} + \omega_{33} b^\dagger_{33} b_{33} + \omega_{34} b^\dagger_{34} b_{34} + \omega_{35} b^\dagger_{35} b_{35} + \omega_{36} b^\dagger_{36} b_{36} + \omega_{37} b^\dagger_{37} b_{37} + \omega_{38} b^\dagger_{38} b_{38} + \omega_{39} b^\dagger_{39} b_{39} + \omega_{4} b^\dagger_{4} b_{4} + \omega_{40} b^\dagger_{40} b_{40} + \omega_{41} b^\dagger_{41} b_{41} + \omega_{42} b^\dagger_{42} b_{42} + \omega_{43} b^\dagger_{43} b_{43} + \omega_{44} b^\dagger_{44} b_{44} + \omega_{45} b^\dagger_{45} b_{45} + \omega_{46} b^\dagger_{46} b_{46} + \omega_{47} b^\dagger_{47} b_{47} + \omega_{48} b^\dagger_{48} b_{48} + \omega_{49} b^\dagger_{49} b_{49} + \omega_{5} b^\dagger_{5} b_{5} + \omega_{50} b^\dagger_{50} b_{50} + \omega_{51} b^\dagger_{51} b_{51} + \omega_{52} b^\dagger_{52} b_{52} + \omega_{53} b^\dagger_{53} b_{53} + \omega_{54} b^\dagger_{54} b_{54} + \omega_{55} b^\dagger_{55} b_{55} + \omega_{56} b^\dagger_{56} b_{56} + \omega_{57} b^\dagger_{57} b_{57} + \omega_{58} b^\dagger_{58} b_{58} + \omega_{59} b^\dagger_{59} b_{59} + \omega_{6} b^\dagger_{6} b_{6} + \omega_{60} b^\dagger_{60} b_{60} + \omega_{61} b^\dagger_{61} b_{61} + \omega_{62} b^\dagger_{62} b_{62} + \omega_{63} b^\dagger_{63} b_{63} + \omega_{64} b^\dagger_{64} b_{64} + \omega_{65} b^\dagger_{65} b_{65} + \omega_{66} b^\dagger_{66} b_{66} + \omega_{67} b^\dagger_{67} b_{67} + \omega_{68} b^\dagger_{68} b_{68} + \omega_{69} b^\dagger_{69} b_{69} + \omega_{7} b^\dagger_{7} b_{7} + \omega_{70} b^\dagger_{70} b_{70} + \omega_{71} b^\dagger_{71} b_{71} + \omega_{72} b^\dagger_{72} b_{72} + \omega_{73} b^\dagger_{73} b_{73} + \omega_{74} b^\dagger_{74} b_{74} + \omega_{75} b^\dagger_{75} b_{75} + \omega_{76} b^\dagger_{76} b_{76} + \omega_{77} b^\dagger_{77} b_{77} + \omega_{78} b^\dagger_{78} b_{78} + \omega_{79} b^\dagger_{79} b_{79} + \omega_{8} b^\dagger_{8} b_{8} + \omega_{80} b^\dagger_{80} b_{80} + \omega_{81} b^\dagger_{81} b_{81} + \omega_{82} b^\dagger_{82} b_{82} + \omega_{83} b^\dagger_{83} b_{83} + \omega_{84} b^\dagger_{84} b_{84} + \omega_{85} b^\dagger_{85} b_{85} + \omega_{86} b^\dagger_{86} b_{86} + \omega_{87} b^\dagger_{87} b_{87} + \omega_{88} b^\dagger_{88} b_{88} + \omega_{89} b^\dagger_{89} b_{89} + \omega_{9} b^\dagger_{9} b_{9} + \omega_{90} b^\dagger_{90} b_{90} + \omega_{91} b^\dagger_{91} b_{91} + \omega_{92} b^\dagger_{92} b_{92} + \omega_{93} b^\dagger_{93} b_{93} + \omega_{94} b^\dagger_{94} b_{94} + \omega_{95} b^\dagger_{95} b_{95} + \omega_{96} b^\dagger_{96} b_{96} + \omega_{97} b^\dagger_{97} b_{97} + \omega_{98} b^\dagger_{98} b_{98} + \omega_{99} b^\dagger_{99} b_{99} + t_{LE, CS} a^{\dagger}_{0} + t_{LE, CS} a_{0} + ε a^{\dagger}_{0} a_{0} + ω_{R} b^\dagger_{1} b_{1}$
Setup Hamiltonian
[8]:
potential = [
[{(tuple((i, i) for i in range(0, ndim))): TensorOperator(mpo=pot_mpo)}]
]
H = TensorHamiltonian(
ndof=len(basis), potential=potential, kinetic=None, backend=backend
)
operators = {"hamiltonian": H}
for i in range(1, ndim):
core = np.zeros((1, basis[i].nprim, 1))
core[0, :, 0] = np.arange(basis[i].nprim)
n = TensorHamiltonian(
ndof=len(basis),
potential=[[{(i,): TensorOperator(mpo=[core], legs=(i,))}]],
kinetic=None,
backend=backend,
)
operators[f"N{i}"] = n
Setup Model (basis, operators, initial states)
[9]:
model = Model(basinfo=basinfo, operators=operators)
model.m_aux_max = 20
init_boson = [[1.0] + [0.0] * (basis[1].nprim - 1)]
model.init_HartreeProduct = [[[1.0, 0.0]] + init_boson * (ndim - 1)]
Execution
[10]:
jobname = "donor-acceptor_model-A"
simulator = Simulator(jobname=jobname, model=model, backend=backend, verbose=2)
simulator.propagate(
maxstep=1000,
stepsize=0.2,
reduced_density=(
[(0, 0)],
10,
),
energy=True,
autocorr=False,
observables=True,
observables_per_step=10,
)
19:30:14 | INFO | Log file is ./donor-acceptor_model-A_prop/main.log
19:30:14 | INFO | Wave function is saved in wf_donor-acceptor_model-A.pkl
19:30:14 | INFO | Start initial step 0.000 [fs]
19:30:19 | INFO | End 0 step; propagated 0.200 [fs]; AVG Krylov iteration: 4.98
19:33:11 | INFO | End 100 step; propagated 20.200 [fs]; AVG Krylov iteration: 4.98
19:36:00 | INFO | End 200 step; propagated 40.200 [fs]; AVG Krylov iteration: 4.98
19:38:46 | INFO | End 300 step; propagated 60.200 [fs]; AVG Krylov iteration: 4.98
19:41:33 | INFO | End 400 step; propagated 80.200 [fs]; AVG Krylov iteration: 4.98
19:44:19 | INFO | End 500 step; propagated 100.200 [fs]; AVG Krylov iteration: 4.98
19:47:05 | INFO | End 600 step; propagated 120.200 [fs]; AVG Krylov iteration: 4.98
19:49:53 | INFO | End 700 step; propagated 140.200 [fs]; AVG Krylov iteration: 4.98
19:52:42 | INFO | End 800 step; propagated 160.200 [fs]; AVG Krylov iteration: 4.98
19:55:31 | INFO | End 900 step; propagated 180.200 [fs]; AVG Krylov iteration: 4.98
19:58:14 | INFO | Saved wavefunction 199.800 [fs]
19:58:15 | INFO | End 999 step; propagated 199.800 [fs]; AVG Krylov iteration: 4.98
19:58:15 | INFO | End simulation and save wavefunction
19:58:15 | INFO | Wave function is saved in wf_donor-acceptor_model-A.pkl
[10]:
(-2.8210573035307007e-09, <pytdscf.wavefunction.WFunc at 0x120622ba0>)
Check results (reduced densities)
[11]:
import netCDF4 as nc
from pytdscf.util import read_nc
data = read_nc(f"{jobname}_prop/reduced_density.nc", [(0,0)])
time_data = data["time"]
density_data_real = data[(0,0)].real
density_data_imag = data[(0,0)].imag
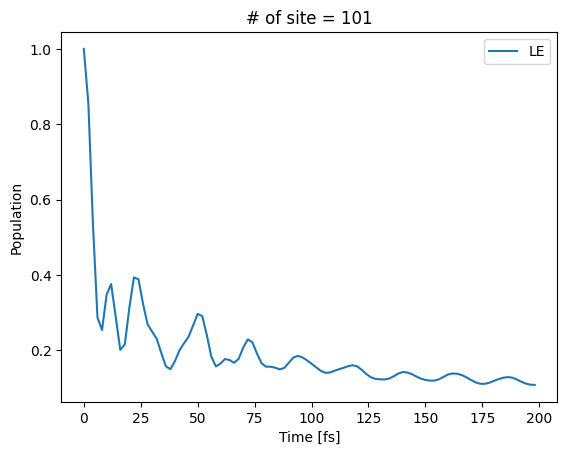
[12]:
plt.title(f"# of site = {len(basis)}")
plt.ylabel("Population")
plt.xlabel("Time [fs]")
plt.plot(time_data, density_data_real[:, 0, 0], label="LE")
plt.legend()
plt.show()
[13]:
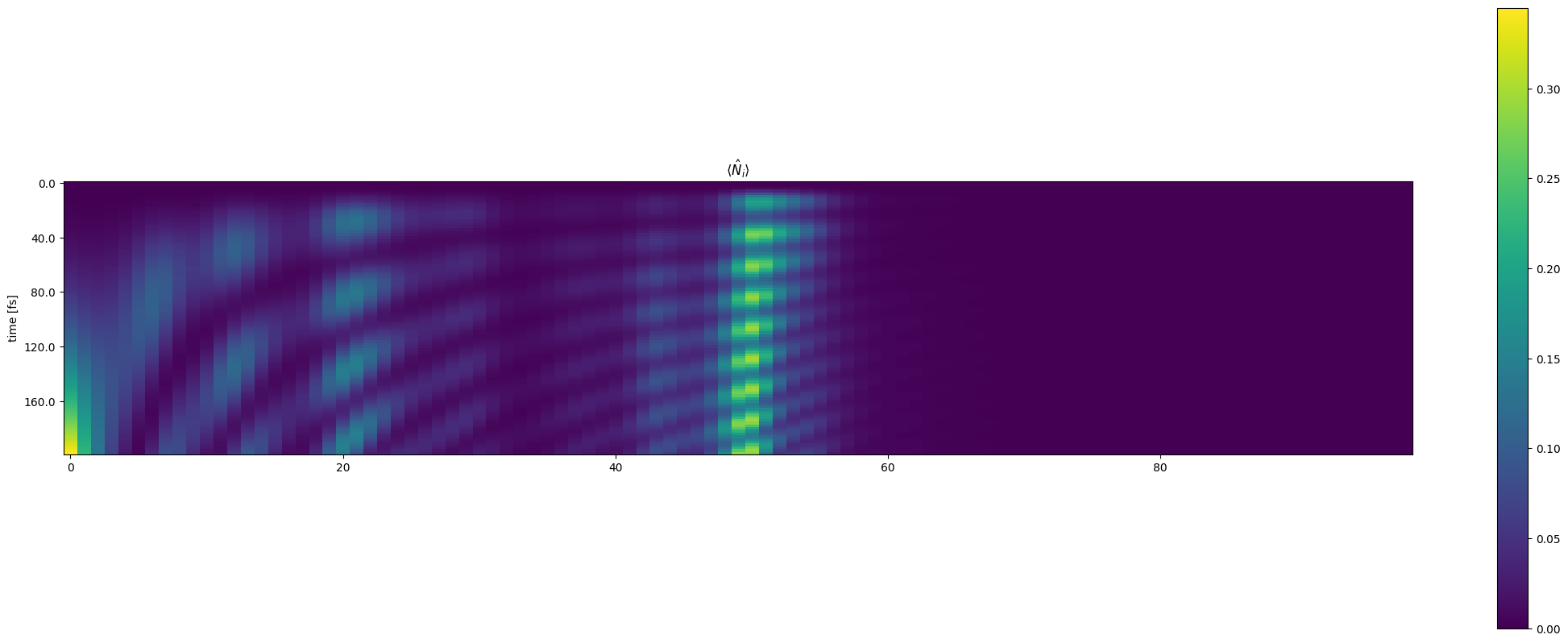
import re
import polars as pl
path = f"{jobname}_prop/expectations.dat"
with open(path, "r") as f:
header = f.readline().strip()
columns = re.split(r"\s+", header)
columns.pop(2)
columns = [columns[1]] + columns[2:]
data = f.readlines()
df = pl.read_csv(
path,
separator="\t",
new_columns=columns,
has_header=False,
skip_rows=1,
schema_overrides={col: pl.Float64 for col in columns},
)
plt.figure(figsize=(27, 10))
plt.imshow(df[columns[2:]], aspect=0.2)
plt.colorbar()
plt.yticks(np.arange(len(df))[::20], df["time"][::20])
plt.ylabel("time [fs]")
plt.title(r"$\langle \hat{N}_i \rangle$")
plt.show()
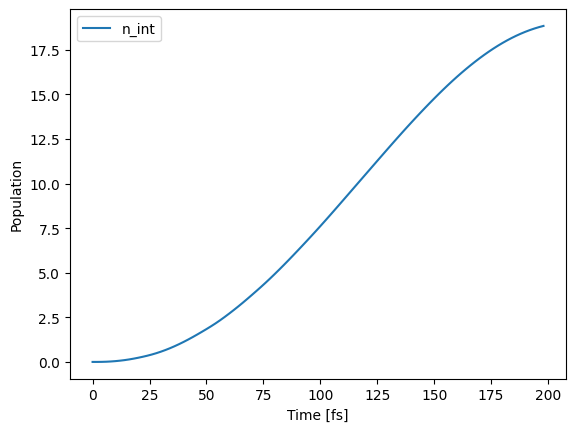
[14]:
plt.ylabel("Population")
plt.xlabel("Time [fs]")
plt.plot(time_data, df[columns[1]], label="n_int") # Intermolecular mode
plt.legend()
plt.show()
[ ]: